Welcome to Subhanil Sir's portal: Harmonic Progression(HP)

In mathematics, the harmonic series is the infinite series

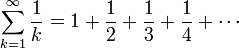$\sum_{k=1}^\infty \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots\,\!$ .

Its name derives from the concept of overtones, or harmonics, in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc. of the string's fundamental wavelength (see harmonic series (music)). Every term of the series after the first is the harmonic mean of the neighboring terms; the term "harmonic mean" also is derived ultimately from music.

The harmonic series diverges, albeit rather slowly, to infinity (the first 10⁴¹ terms sum to less than 100). One way to prove the divergence is by noting that the harmonic series is term-by-term larger than or equal to another divergent series

$\sum_{k=1}^\infty \frac{1}{k} = 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{3} + \frac{1}{4}\right] + \left[\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}\right] + \left[\frac{1}{9}+\cdots\right.$

$\quad\ \ge \sum_{k=1}^\infty 2^{-\lceil \log_2 k \rceil}\,\!$

$= 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{4} + \frac{1}{4}\right] + \left[\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\right] + \left[\frac{1}{16}+\cdots\right.\,\!$

$= 1 +\ \frac{1}{2}\ + \qquad\frac{1}{2} \ \quad+ \ \qquad\quad\frac{1}{2}\qquad\ \quad \ + \ \quad\ \cdots \,\!$

which clearly diverges. (Both sets of grouping can rigorously be imposed since all terms in each series have the same sign.) This proof, due to Nicole Oresme, is a high point of medieval mathematics.

Even the sum of the reciprocals of the prime numbers diverges to infinity (although that is much harder to prove; see this article for the details).

Convergence of the alternating harmonic series

The alternating harmonic series converges:

$\sum_{k = 1}^\infty \frac{(-1)^{k + 1}}{k} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots = \ln 2 = 0.69314718\dots$

This equality is a consequence of the Mercator series, the Taylor series for the natural logarithm. Another very interesting equality, similar in form to Mercator's series is:

$\sum_{k=0}^\infty \frac{(-1)^k}{2k+1} = 1 - \frac{1}{3} + \frac{1}{5} -\frac{1}{7} +\cdots = \frac{\pi}{4}.$

Partial sums

The nth partial sum of the diverging harmonic series,

$H_n = \sum_{k = 1}^n \frac{1}{k}$

is called the nth harmonic number.

The difference between distinct harmonic numbers is never an integer.

Jeffrey Lagarias proved in 2001 that the Riemann hypothesis is logically equivalent to the statement

$\sigma(n)\le H_n + \ln(H_n)e^{H_n} \qquad \mbox{ for every }n\in\mathbb{N}$

where σ(n) stands for the sum of the positive divisors of n.^[1]

General harmonic series

The general harmonic series is of the form

$\sum_{n=1}^{\infty}\frac{1}{an+b}.$

All general harmonic series diverge.

"p-series"

The p-series, is (any of) the series

$\sum_{n=1}^{\infty}\frac{1}{n^p}$

for p a positive real number. The series is always convergent if p > 1 and divergent otherwise. When p = 1, the series is the harmonic series. If p > 1 then the sum of the series is ζ(p), i.e., the Riemann zeta function evaluated at p.

Random harmonic series

Byron Schmuland of the University of Alberta examined^[2]^[3] the properties of the random harmonic series

$\sum_{n=1}^{\infty}\frac{s_{n}}{n}$

where the s_n are independent, identically distributed random variables taking the values +1 and −1 with equal probability 1/2. He shows that this sum converges with probability 1 and that the convergent is a random variable with some interesting properties. In particular, the probability density function of this random variable evaluated at +2 or at −2 takes on the value 0.1249999999999999999999999999999999999999997642..., differing from 1/8 by less than 10⁻⁴². Schmuland's paper actually explains why this probability is so close to, but not exactly, 1/8.