The function F(x) = x3/3 is an antiderivative of f(x) = x2. As the derivative of a constant is zero, x2 will have an infinite number of antiderivatives; such as (x3/3) + 0, (x3 / 3) + 7, (x3 / 3) − 36, etc. Thus, the antiderivative family of x2 is collectively referred to by F(x) = (x3 / 3) + C; where C is an arbitrary constant known as the constant of integration. Essentially, the graphs of antiderivatives of a given function are vertical translations of each other; each graph's location depending upon the value of C.
Antiderivatives are important because they can be used to compute definite integrals, using the fundamental theorem of calculus: if F is an antiderivative of the integrable function f, then:
Because of this, the set of all antiderivatives of a given function f is sometimes called the general integral or indefinite integral of f and is written using the integral symbol with no bounds:
It is critical to remember that an integral is not the same, in general, as the means for evaluating it; and the function that an integral implies stands apart from that means - in the case of single-variable integrals, from antiderivatives.
If F is an antiderivative of f, and the function f is defined on some interval, then every other antiderivative G of f differs from F by a constant: there exists a number C such that G(x) = F(x) + C for all x. C is called the arbitrary constant of integration. If the domain of F is a disjoint union of two or more intervals, then a different constant of integration may be chosen for each of the intervals. For instance
 0\end{cases}">
0\end{cases}">
is the most general antiderivative of f(x) = 1 / x2 on its natural domain 
Every continuous function f has an antiderivative, and one antiderivative F is given by the definite integral of f with variable upper boundary:
Varying the lower boundary produces other antiderivatives (but not necessarily all possible antiderivatives). This is another formulation of the fundamental theorem of calculus.
There are many functions whose antiderivatives, even though they exist, cannot be expressed in terms of elementary functions (like polynomials, exponential functions, logarithms, trigonometric functions, inverse trigonometric functions and their combinations). Examples of these are
Let f and g be functions. Now consider:
By the sum rule in integration, this is
By the constant factor rule in integration, this reduces to
Hence we have
Suppose f(x) is an integrable function, and φ(t) is a continuously differentiable function which is defined on the interval [a, b] and whose image (also known as range) is contained in the domain of f.
Suppose the derivative φ'(t) is integrable on [a,b] and
Then
The formula is best remembered using Leibniz notation: the substitution x = φ(t) yields dx / dt = φ'(t) and thus formally dx = φ'(t) dt, which is precisely the required substitution for dx. (In fact, one may view the substitution rule as a major justification of Leibniz's notation for integrals and derivatives.)
The formula is used to transform one integral into another integral that is easier to compute. Thus, the formula can be used from left to right or from right to left in order to simplify a given integral. When used in the latter manner, it is sometimes known as u-substitution.
Proof of the substitution rule
We will now prove the substitution rule for definite integrals. Let F be an antiderivative of f so F'(x) = f(x). By the fundamental theorem of calculus,
Next we define a function G by the rule
Then by the Chain rule G is differentiable with derivative
Integrating both sides with respect to x and using the Fundamental Theorem of Calculus we get
But by the definition of F this equals
Hence
which is the substitution rule for definite integrals.
Examples
Consider the integral
By using the substitution u = x2 + 1, we obtain du = 2x dx and
Here we used the substitution rule from right to left. Note how the lower limit x = 0 was transformed into u = 02 + 1 = 1 and the upper limit x = 2 into u = 22 + 1 = 5.
For the integral
the formula needs to be used from left to right: the substitution x = sin(u), dx = cos(u) du is useful, because √(1-sin2(u)) = cos(u):
The resulting integral can be computed using integration by parts or a double angle formula followed by one more substitution.
Antiderivatives
The substitution rule can be used to determine antiderivatives. One chooses a relation between x and u, determines the corresponding relation between dx and du by differentiating, and performs the substitutions. An antiderivative for the substituted function can hopefully be determined; the original substitution between x and u is then undone.
Similar to our first example above, we can determine the following antiderivative with this method:
where C is an arbitrary constant of integration.
Note that there were no integral boundaries to transform, but in the last step we had to revert the original substitution x = u2 + 1.
Substitution rule for multiple variables
One may also use substitution when integrating functions of several variables. Here the substitution function (v1,...,vn) = φ(u1,...,un ) needs to be one-to-one and continuously differentiable, and the differentials transform as
where det(Dφ)(u1,...,un ) denotes the determinant of the Jacobian matrix containing the partial derivatives of φ . This formula expresses the fact that the absolute value of the determinant of given vectors equals the volume of the spanned parallelepiped.
More precisely, the change of variables formula is stated in the following theorem:
Theorem. Let U, V be open sets in Rn and φ : U → V an injective differentiable function with continuous partial derivatives, the Jacobian of which is nonzero for every x in U. Then for any real-valued, compactly supported, continuous function f, with support connected in φ(U),
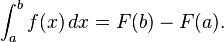
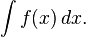




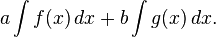

![\phi'(t) \ne 0 \quad \mbox{ for all } t \mbox{ in } [a,b].](http://upload.wikimedia.org/math/b/f/5/bf58696e6df321cd911c62417882c50e.png)




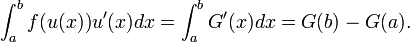
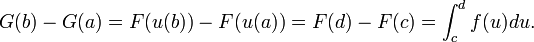
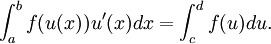
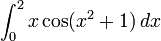

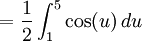


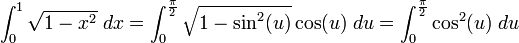




No comments:
Post a Comment