Tuesday, May 15, 2007

All About Vectors

A vector going from A to B.
A vector going from A to B.

In physics and in vector calculus, a spatial vector, or simply vector, is a concept characterized by a magnitude and a direction.

A spatial vector can be formally defined by its relationship to the spatial coordinate system under rotations. Alternatively, it can be defined in a coordinate-free fashion via a tangent space of a three-dimensional manifold in the language of differential geometry. These definitions are discussed in more detail below.

A spatial vector is a special case of a tensor and is also analogous to a four-vector in relativity (and is sometimes therefore called a three-vector in reference to the three spatial dimensions, although this term also has another meaning for p-vectors of differential geometry). Vectors are the building blocks of vector fields and vector calculus.


Informally, a vector is a quantity characterized by a magnitude (in mathematics a number, in physics a number times a unit) and a direction, often represented graphically by an arrow. Examples are "moving north at 90 km/h" or "pulling towards the center of Earth with a force of 70 newtons".

The notion of having a "magnitude" and "direction" is formalized by saying that the vector has components that transform like the coordinates under rotations. That is, if the coordinate system undergoes a rotation described by a rotation matrix R, so that a coordinate vector x is transformed to x′ = Rx, then any other vector v is similarly transformed via v′ = Rv. This ensures the invariance of the operations dot product, Euclidean norm, cross product, gradient, divergence, curl, and scalar triple product, and trivially for vector addition and subtraction, and scalar multiplication. The terms scalar and vector as used here include pseudoscalars and pseudovectors or axial vectors.

More generally, a vector is a tensor of contravariant rank one. In differential geometry, the term vector usually refers to quantities that are closely related to tangent spaces of a differentiable manifold (assumed to be three-dimensional and equipped with a positive definite Riemannian metric). (A four-vector is a related concept when dealing with a 4 dimensional spacetime manifold in relativity.)

Examples of vectors include displacement, velocity, electric field, momentum, force, and acceleration.

Vectors can be contrasted with scalar quantities such as distance, speed, energy, time, temperature, charge, power, work, and mass, which have magnitude, but no direction (they are invariant under coordinate rotations). The magnitude of any vector is a scalar.

A related concept is that of a pseudovector (or axial vector). This is a quantity that transforms like a vector under proper rotations, but gains an additional sign flip under improper rotations. Examples of pseudovectors include magnetic field, torque, and angular momentum. (This distinction between vectors and pseudovectors is often ignored, but it becomes important in studying symmetry properties.) To distinguish from pseudo/axial vectors, an ordinary vector is sometimes called a polar vector. See also parity (physics).

Sometimes, one speaks informally of bound or fixed vectors, which are vectors additionally characterized by a "base point". Most often, this term is used for position vectors (relative to an origin point). More generally, however, the physical interpretation of a particular vector can be parameterized by any number of quantities.

Examples in one dimension

A force may be "15 N to the right", with coordinate 15 N if the basis vector is to the right, and −15 N if the basis vector is to the left. The magnitude of the vector is 15 N in both cases. A displacement may be "4 m to the right", with coordinate 4 m if the basis vector is to the right, and −4 m if the basis vector is to the left. The magnitude of the vector is 4 m in both cases. The work done by the force in the case of this displacement is 60 J in both cases.

The force and displacement are vectors, the magnitudes are scalars, and the coordinates are neither.

Generalizations

In mathematics, a vector is considered more than a representation of a physical quantity. In general, a vector is any element of a vector space over some field. The spatial vectors of this article are a very special case of this general definition (they are not simply any element of Rd in d dimensions), which includes a variety of mathematical objects (algebras, the set of all functions from a given domain to a given linear range, and linear transformations). Note that under this definition, a tensor is a special vector.

Representation of a vector

Vectors are usually denoted in boldface, as a. Other conventions include 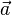\vec{a} or a, especially in handwriting. Alternately, some use a tilde (~) or a wavy underline drawn beneath the symbol, which is a convention for indicating boldface type.

Vectors are usually shown in graphs or other diagrams as arrows, as illustrated below:

Vector arrow pointing from A to B

Here the point A is called the tail, base, start, or origin; point B is called the head, tip, endpoint, or destination. The length of the arrow represents the vector's magnitude, while the direction in which the arrow points represents the vector's direction.

In the figure above, the arrow can also be written as \overrightarrow{AB} or AB.

On a two-dimensional diagram, sometimes a vector perpendicular to plane of the diagram is desired. These vectors are commonly shown as small circles. A circle with a dot at its centre indicates a vector pointing out of the front of the diagram, towards the viewer. A circle with a cross inscribed in it indicates a vector pointing into and behind the diagram. These can be thought of as viewing the tip an arrow front on and viewing the vanes of an arrow from the back.

Vectors pointing into (left) and out of (right) the plane

The length or magnitude or norm of the vector a is denoted by |a|.

If a vector is itself spatial, the length of the arrow depends on a dimensionless scale. If it represents e.g. a force, the "scale" is of physical dimension length/force. Thus there is typically consistency in scale among quantities of the same dimension, but otherwise scale ratios may vary; for example, if "1 newton" and "5 m" are both represented with an arrow of 2 cm, the scales are 1:250 and 1 m:50 N respectively. Equal length of vectors of different dimension has no particular significance unless there is some proportionality constant inherent in the system that the diagram represents. Also length of a unit vector (of dimension length, not length/force, etc.) has no coordinate-system-invariant significance.

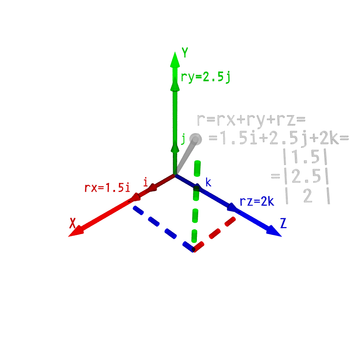
In order to calculate with vectors, the graphical representation may be too cumbersome. Vectors in a n-dimensional Euclidean space can be represented as a linear combination of n mutually perpendicular unit vectors (the basis ). In this article, we will consider R3 as an example. In R3, we usually denote three orthogonal unit vectors by e1, e2 and e3 respectively (orthogonal unit vectors are often denoted i, j, k but that ancient notation clashes with the index notation and the summation convention commonly used in many areas of mathematics, physics and engineering). Any vector a in R3 can be written as a = a1 e1 + a2 e2 + a3 e3 with real numbers a1, a2 and a3 (the components ) which are uniquely determined by a and the choice of basis vectors e1, e2 and e3 . Sometimes a is then also written as a 3-by-1 or 1-by-3 matrix:

\mathbf{a} = \begin{bmatrix} a_1\\ a_2\\ a_3\\ \end{bmatrix}
\mathbf{a} = \langle a_1\ a_2\ a_3 \rangle

even though this notation suppresses the dependence of the components a1, a2 and a3 on the specific choice of orthogonal unit vectors e1, e2 and e3. [Note: a basis does not need to be orthogonal, any set of three linearly independent vectors will do, but a set of orthogonal unit vectors is particularly convenient for operations such as the dot product of two vectors and determining the length of a vector from its components].

Length of a vector

The length of the vector a = a1e1 + a2e2+ a3e3 in a three-dimensional Euclidean space, where e1, e2, e3 are orthogonal unit vectors, can be computed with the Euclidean norm

\left\|\mathbf{a}\right\|=\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}

which is a consequence of the Pythagorean theorem since the basis vectors e1 , e2 , e3 are orthogonal unit vectors.

This happens to be equal to the square root of the dot product of the vector with itself:

\left\|\mathbf{a}\right\|=\sqrt{\mathbf{a}\cdot\mathbf{a}}

Vector equality

Two vectors are said to be equal if they have the same magnitude and direction. However if we are talking about bound vector, then two bound vectors are equal if they have the same base point and end point.

For example, the vector i + 2j + 3k with base point (1,0,0) and the vector i+2j+3k with base point (0,1,0) are different bound vectors, but the same (displacement) vector.

Vector addition and subtraction

Let a=a1e1 + a2e2 + a3e3 and b=b1e1 + b2e2 + b3e3, where e1, e2, e3 are orthogonal unit vectors (Note: they only need to be linearly independent, i.e. not parallel and not in the same plane, for these algebraic addition and subtraction rules to apply)

The sum of a and b is:

\mathbf{a}+\mathbf{b} =(a_1+b_1)\mathbf{e_1} +(a_2+b_2)\mathbf{e_2} +(a_3+b_3)\mathbf{e_3}

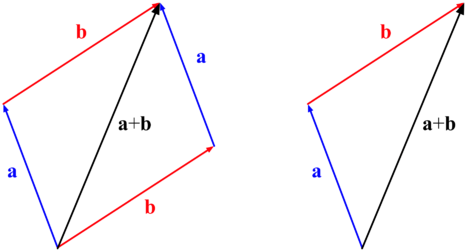
The addition may be represented graphically by placing the start of the arrow b at the tip of the arrow a, and then drawing an arrow from the start of a to the tip of b. The new arrow drawn represents the vector a + b, as illustrated below:

The addition of two vectors a and b

This addition method is sometimes called the parallelogram rule because a and b form the sides of a parallelogram and a + b is one of the diagonals. If a and b are bound vectors, then the addition is only defined if a and b have the same base point, which will then also be the base point of a + b. One can check geometrically that a + b = b + a and (a + b) + c = a + (b + c).

The difference of a and b is:

\mathbf{a}-\mathbf{b} =(a_1-b_1)\mathbf{e_1} +(a_2-b_2)\mathbf{e_2} +(a_3-b_3)\mathbf{e_3}

Subtraction of two vectors can be geometrically defined as follows: to subtract b from a, place the ends of a and b at the same point, and then draw an arrow from the tip of b to the tip of a. That arrow represents the vector a − b, as illustrated below:

The subtraction of two vectors a and b

If a and b are bound vectors, then the subtraction is only defined if they share the same base point which will then also become the base point of their difference. This operation deserves the name "subtraction" because (a − b) + b = a.

In physics, vectors of different physical dimension may occur in the same diagram. However, adding or subtracting them (graphically or otherwise) is meaningless.

Scalar multiplication

A vector may also be multiplied by a real number r. In mathematics, numbers are often called scalars to distinguish them from vectors, and this operation is therefore called scalar multiplication. The resulting vector is:

r\mathbf{a}=(ra_1)\mathbf{e_1} +(ra_2)\mathbf{e_2} +(ra_3)\mathbf{e_3}

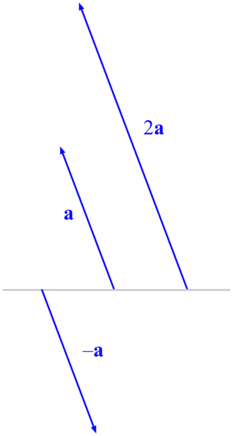
The length of ra is |r||a|. If the scalar is negative, it also changes the direction of the vector by 180o. Two examples (r = -1 and r = 2) are given below:

The scalar multiplications 2a and −a of a vector a

Here it is important to check that the scalar multiplication is compatible with vector addition in the following sense: r(a + b) = ra + rb for all vectors a and b and all scalars r. One can also show that a - b = a + (-1)b.

The set of all geometrical vectors, together with the operations of vector addition and scalar multiplication, satisfies all the axioms of a vector space. Similarly, the set of all bound vectors with a common base point forms a vector space. This is where the term "vector space" originated.

In physics, scalars also have a unit. The scale of acceleration in the diagram is e.g. 2 m/s² : cm, and that of force 5 N : cm. Thus a scale ratio of 2.5 kg : 1 is used for mass. Similarly, if displacement has a scale of 1:1000 and velocity of 0.2 cm : 1 m/s, or equivalently, 2 ms : 1, a scale ratio of 0.5 : s is used for time.

Unit vector

Unit vector a.k.a. Direction vector

A unit vector is any vector with a length of one, geometrically, it only indicates a direction but no magnitude. If you have a vector of arbitrary length, you can divide it by its length to create a unit vector. This is known as normalizing a vector. A unit vector is often indicated with a hat as in â.

The normalization of a vector a into a unit vector â

To normalize a vector a = [a1, a2, a3], scale the vector by the reciprocal of its length ||a||. That is:

\mathbf{\hat{a}} = \frac{\mathbf{a}}{\left\|\mathbf{a}\right\|} = \frac{a_1}{\left\|\mathbf{a}\right\|}\mathbf{e_1} + \frac{a_2}{\left\|\mathbf{a}\right\|}\mathbf{e_2} + \frac{a_3}{\left\|\mathbf{a}\right\|}\mathbf{e_3}

Dot product

Main article: Dot product

The dot product of two vectors a and b (sometimes called inner product, or, since its result is a scalar, the scalar product) is denoted by a ∙ b and is defined as:

\mathbf{a}\cdot\mathbf{b} =\left\|\mathbf{a}\right\|\left\|\mathbf{b}\right\|\cos\theta

where ||a|| and ||b|| denote the norm (or length) of a and b, and θ is the measure of the angle between a and b (see trigonometric function for an explanation of cosine). Geometrically, this means that a and b are drawn with a common start point and then the length of a is multiplied with the length of that component of b that points in the same direction as a.

The dot product can also be defined as the sum of the products of the components of each vector:

\mathbf{a} \cdot \mathbf{b} = \langle a_1, a_2, \dots, a_n \rangle \cdot \langle b_1, b_2, \dots, b_n \rangle = a_1 b_1 + a_2 b_2 + \dots + a_n b_n

where a and b are vectors of n dimensions; a1, a2, …, an are coordinates of a; and b1, b2, …, bn are coordinates of b.

This operation is often useful in physics; for instance, work is the dot product of force and displacement.

Cross product


The cross product (also vector product or outer product) differs from the dot product primarily in that the result of a cross product of two vectors is a vector. While everything that was said above can be generalized in a straightforward manner to more than three dimensions, the cross product is only meaningful in three dimensions, although the seven dimensional cross product is similar in some respects. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as:

\mathbf{a}\times\mathbf{b} =\left\|\mathbf{a}\right\|\left\|\mathbf{b}\right\|\sin(\theta)\,\mathbf{n}

where θ is the measure of the angle between a and b, and n is a unit vector perpendicular to both a and b. The problem with this definition is that there are two unit vectors perpendicular to both b and a.

An illustration of the cross product.
An illustration of the cross product.

The vector basis e1, e2 , e3 is called right handed, if the three vectors are situated like the thumb, index finger and middle finger (pointing straight up from your palm) of your right hand. Graphically the cross product can be represented by the figure on the right.

The cross product a × b is defined so that a, b, and a × b also becomes a right handed system (but note that a and b are not necessarily orthogonal). This is the right-hand rule.

Because the cross product depends on the choice of handedness it changes sign under mirror reflection (P-symmetry), its result is referred to as a pseudovector. In physics, cross products tend to come in pairs, so that the "handedness" of the cross product is undone by a second cross product.

The length of a × b can be interpreted as the area of the parallelogram having a and b as sides.

Scalar triple product

The scalar triple product (also called the box product or mixed triple product) isn't really a new operator, but a way of applying the other two multiplication operators to three vectors. The scalar triple product is denoted by (a b c) and defined as:

(\mathbf{a}\ \mathbf{b}\ \mathbf{c}) =\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})

It has three primary uses. First, the absolute value of the box product is the volume of the parallelepiped which has edges that are defined by the three vectors. Second, the scalar triple product is zero if and only if the three vectors are linearly dependent, which can be easily proved by considering that in order for the three vectors to not make a volume, they must all lie in the same plane. Third, the box product is positive if and only if the three vectors a, b and c are right-handed.

In components ( with respect to a right-handed orthonormal basis), if the three vectors are thought of as rows (or columns, but in the same order), the scalar triple product is simply the determinant of the 3-by-3 matrix having the three vectors as rows. The scalar triple product is linear in all three entries and anti-symmetric in the following sense:

(\mathbf{a}\ \mathbf{b}\ \mathbf{c}) =(\mathbf{c}\ \mathbf{a}\ \mathbf{b})

=(\mathbf{b}\ \mathbf{c}\ \mathbf{a})

=-(\mathbf{a}\ \mathbf{c}\ \mathbf{b})

=-(\mathbf{b}\ \mathbf{a}\ \mathbf{c})

=-(\mathbf{c}\ \mathbf{b}\ \mathbf{a})

Technically, the scalar triple product is not a scalar, it is a pseudoscalar since handedness comes into its definiton. It changes sign under inversion (that is when x goes to −x).

Vector components

Illustration of tangential and normal components of a vector to a surface.
Illustration of tangential and normal components of a vector to a surface.

A component of a vector is the influence of that vector in a given direction. [1] Components are themselves vectors.

A vector is often described by a fixed number of components that sum up into this vector uniquely and totally. When used in this role, the choice of their constituting directions is dependent upon the particular coordinate system being used, such as Cartesian coordinates, spherical coordinates or polar coordinates. For example, axial component of a vector is such its component whose direction is determined by one of the Cartesian coordinate axes, whereas radial and tangential components relate to the radius of rotation of an object as their direction of reference. The former is parallel to the radius and the latter is orthogonal to it. [2] Both remain orthogonal to the axis of rotation at all times. (In two dimensions this requirement becomes redundant as the axis degenerates to a point of rotation.) The choice of a coordinate system doesn't affect properties of a vector or its behaviour under transformations.

Vectors as directional derivatives

A vector may also be defined as a directional derivative: consider a function f(xα) and a curve xα(σ). Then the directional derivative of f is a scalar defined as

\frac{df}{d\sigma} = \frac{dx^\alpha}{d\sigma}\frac{\partial f}{\partial x^\alpha}.

where the index α is summed over the appropriate number of dimensions (e.g. from 1 to 3 in 3-dimensional Euclidian space, from 0 to 3 in 4-dimensional spacetime, etc.). Then consider a vector tangent to xα(σ):

t^\alpha = \frac{dx^\alpha}{d\sigma}.

We can rewrite the directional derivative in differential form (without a given function f) as

\frac{d}{d\sigma} = t^\alpha\frac{\partial}{\partial x^\alpha}.

Therefore any directional derivative can be identified with a corresponding vector, and any vector can be identified with a corresponding directional derivative. We can therefore define a vector precisely:

\mathbf{a} \equiv a^\alpha \frac{\partial}{\partial x^\alpha}.






Posted by at

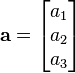
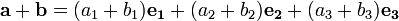
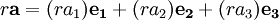
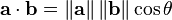
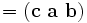
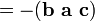
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)