In mathematics, the harmonic series is the infinite series
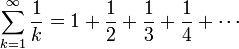 .
.
Its name derives from the concept of overtones, or harmonics, in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc. of the string's fundamental wavelength (see harmonic series (music)). Every term of the series after the first is the harmonic mean of the neighboring terms; the term "harmonic mean" also is derived ultimately from music.
The harmonic series diverges, albeit rather slowly, to infinity (the first 1041 terms sum to less than 100). One way to prove the divergence is by noting that the harmonic series is term-by-term larger than or equal to another divergent series
which clearly diverges. (Both sets of grouping can rigorously be imposed since all terms in each series have the same sign.) This proof, due to Nicole Oresme, is a high point of medieval mathematics.
Even the sum of the reciprocals of the prime numbers diverges to infinity (although that is much harder to prove; see this article for the details).Convergence of the alternating harmonic series
The alternating harmonic series converges:
This equality is a consequence of the Mercator series, the Taylor series for the natural logarithm. Another very interesting equality, similar in form to Mercator's series is:
Partial sums
The nth partial sum of the diverging harmonic series,
is called the nth harmonic number.
The difference between distinct harmonic numbers is never an integer.
Jeffrey Lagarias proved in 2001 that the Riemann hypothesis is logically equivalent to the statement
where σ(n) stands for the sum of the positive divisors of n.[1]
General harmonic series
The general harmonic series is of the form
All general harmonic series diverge.
"p-series"
The p-series, is (any of) the series
for p a positive real number. The series is always convergent if p > 1 and divergent otherwise. When p = 1, the series is the harmonic series. If p > 1 then the sum of the series is ζ(p), i.e., the Riemann zeta function evaluated at p.
Random harmonic series
Byron Schmuland of the University of Alberta examined[2][3] the properties of the random harmonic series
where the sn are independent, identically distributed random variables taking the values +1 and −1 with equal probability 1/2. He shows that this sum converges with probability 1 and that the convergent is a random variable with some interesting properties. In particular, the probability density function of this random variable evaluated at +2 or at −2 takes on the value 0.1249999999999999999999999999999999999999997642..., differing from 1/8 by less than 10−42. Schmuland's paper actually explains why this probability is so close to, but not exactly, 1/8.
![\sum_{k=1}^\infty \frac{1}{k} = 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{3} + \frac{1}{4}\right] + \left[\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}\right] + \left[\frac{1}{9}+\cdots\right.](http://upload.wikimedia.org/math/3/4/d/34d0af6be3a04934ee3b8942a3e8bf60.png)

![= 1 + \left[\frac{1}{2}\right] + \left[\frac{1}{4} + \frac{1}{4}\right] + \left[\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\right] + \left[\frac{1}{16}+\cdots\right.\,\!](http://upload.wikimedia.org/math/9/9/c/99c4bb52b8911237298d29c132776878.png)








2 comments:
how to prove then that infinite sum of series1/((2n-1)(2n+1)) = 1/2
how can one prove that partial sum of the infinte series 1/(2n-1)(2n+1) = m/(2m+1)
Post a Comment