Kirchhoff's circuit laws are a pair of laws that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff. Widely used in electrical engineering, they are also called Kirchhoff's rules or simply Kirchhoff's laws (see also Kirchhoff's laws for other meanings of that term).
Both circuit rules can be directly derived from Maxwell's equations, but Kirchhoff preceded Maxwell and instead generalized work by Georg Ohm.
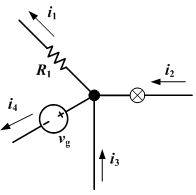
Kirchhoff's Current Law (KCL)
This law is also called Kirchhoff's first law, Kirchhoff's point rule, Kirchhoff's junction rule, and Kirchhoff's first rule.
The principle of conservation of electric charge implies that:
- At any point in an electrical circuit where charge density is not changing in time, the sum of currents flowing towards that point is equal to the sum of currents flowing away from that point.
A charge density changing in time would mean the accumulation of a net positive or negative charge, which typically cannot happen to any significant degree because of the strength of electrostatic forces: the charge buildup would cause repulsive forces to disperse the charges.
However, a charge build up can occur in a capacitor, where the charge is typically spread over wide parallel plates, with a physical break in the circuit that prevents the positive and negative charge accumulations over the two plates from coming together and cancelling. In this case, the sum of the currents flowing into one plate of the capacitor is not zero, but rather is equal to the rate of charge accumulation. However, if the displacement current dD/dt is included, Kirchhoff's current law once again holds. (This is only required if one wants to apply the current law within the capacitor. In circuit analyses, however, the capacitor as a whole is typically treated as a unit, in which case the ordinary current law holds since the net charge is always zero.)
More technically, Kirchhoff's current law can be found by taking the divergence of Ampère's law with Maxwell's correction and combining with Gauss's law, yielding:
This is simply the charge conservation equation (in integral form, it says that the current flowing out of a closed surface is equal to the rate of loss of charge within the enclosed volume). Kirchhoff's current law is equivalent to the statement that the divergence of the current is zero, true for time-invariant ρ, or always true if the displacement current is included with J. This can also be interpreted as a special case of Gauss's law for a small point containing no electric charge.
A matrix version of Kirchhoff's current law is the basis of most circuit simulation software, such as SPICE or NI Multisim.
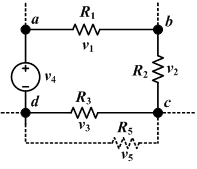
Kirchhoff's Voltage Law (KVL)
This law is also called Kirchhoff's second law, Kirchhoff's loop rule, and Kirchhoff's second rule. It is a consequence of the principle of conservation of energy.
The principle of conservation of energy implies that:
- The directed sum of the electrical potential differences around a circuit must be zero.
(Otherwise, it would be possible to build a perpetual motion machine that passed a current in a circle around the circuit.)
Considering that electric potential is defined as line integral of electric field, Kirchhoff's voltage law can be expressed equivalently with equation
which states that line integral of electric field around closed loop C is zero.
This is a simplification of Faraday's law of induction for the special case where there is no fluctuating magnetic field linking the closed loop. In the presence of a changing magnetic field the electric field is not conservative and it cannot therefore define a pure scalar potential—the line integral of the electric field around the circuit is not zero. This is because energy is being transferred from the magnetic field to the current (or vice versa). In order to "fix" Kirchhoff's voltage law for circuits containing inductors, an effective potential drop, or electromotive force (emf), is associated with each inductance of the circuit, exactly equal to the amount by which the line integral of the electric field is not zero by Faraday's law of induction.
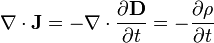

No comments:
Post a Comment