The rule is believed to be the work of Johann Bernoulli since l'Hôpital, a nobleman, paid Bernoulli a retainer of 300₣ per year to keep him updated on developments in calculus and to solve problems he had. Among these problems was that of limits of indeterminate forms. When l'Hôpital published his book, he gave due credit to Bernoulli and, not wishing to take credit for any of the mathematics in the book, he published the work anonymously. Bernoulli, who was known for being extremely jealous, claimed to be the author of the entire work, and until recently, it was believed to be so. Nevertheless, the rule was named for l'Hôpital, who never claimed to have invented it in the first place[1].
The Stolz-Cesàro theorem is a similar result involving limits of sequences, and using finite difference operators rather than derivatives.
Introduction
In simple cases, l'Hôpital's rule states that for functions f(x) and g(x), if:
or
then:
where the prime (') denotes the derivative.
Among other requirements, for this rule to hold, the limit 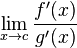 must exist. Other requirements are detailed below, in the formal definition.
must exist. Other requirements are detailed below, in the formal definition.
Formal statement
When determining the limit of a quotient  when both f and g approach 0, or f and g approach infinity, l'Hôpital's rule states that if
when both f and g approach 0, or f and g approach infinity, l'Hôpital's rule states that if 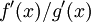 converges, then
converges, then  converges, and to the same limit. This differentiation often simplifies the quotient and/or converts it to a determinate form, allowing the limit to be determined more easily.
converges, and to the same limit. This differentiation often simplifies the quotient and/or converts it to a determinate form, allowing the limit to be determined more easily.
Symbolically let  . Suppose that
. Suppose that  , that
, that
and that  for all
for all  in an open interval (a,b) containing c (or with
in an open interval (a,b) containing c (or with  if
if  or with
or with  if
if  ). If
). If
then
L'Hôpital's rule also holds for one-sided limits.
Basic indeterminate forms (all others reduce to these):

Other indeterminate forms:
Note the requirement that the limit 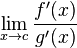 exists. Differentiation of limits of this form can sometimes lead to limits that do not exist. In that case, L'Hôpital's rule cannot be applied. For instance if f(x) = x + sin(x) and g(x) = x, then
exists. Differentiation of limits of this form can sometimes lead to limits that do not exist. In that case, L'Hôpital's rule cannot be applied. For instance if f(x) = x + sin(x) and g(x) = x, then
does not exist, whereas
In practice one often uses the rule and, if the resulting limit exists, concludes that it was legitimate to use l'Hôpital's rule.
Note also the requirement that the derivative of g not vanish throughout an entire interval containing the point c. Without such a hypothesis, the conclusion is false. Thus one must not use l'Hôpital's rule if the denominator oscillates wildly near the point where one is trying to find the limit. For example if f(x) = x + cos(x)sin(x) and g(x) = esin(x)(x + cos(x)sin(x)), then
whereas
does not exist since  fluctuates between e-1 and e.
fluctuates between e-1 and e.
Examples
- Here is an example involving the sinc function, which has the form 0/0 :
- However, it is simpler to observe that this limit is just the definition of the derivative of sin(x) at x = 0.
- In fact this particular limit is needed in the most usual proof that the derivative of sin(x) is cos(x), but we cannot use l'Hôpital's rule to do this, as it would produce a circular argument.
- Here is a more elaborate example involving the indeterminate form 0/0. Applying the rule a single time still results in an indeterminate form. In this case, the limit may be evaluated by applying l'Hôpital's rule three times:
- Here is another case involving 0/0:
- Here is a case of ∞/∞:
- This one involves ∞/∞. Assume n is a positive integer.
- Iterate the above until the exponent is 0. Then one sees that the limit is 0.
- This one also involves ∞/∞:
- The previous result can be used the following case of the indeterminate form 00: To compute
 , we rewrite xx as exlnx and get
, we rewrite xx as exlnx and get
- This is the impulse response of a raised-cosine filter:
- And:
With the indeterminate form 0 over 0
The case when 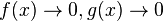
First, we expand continuously (or redefine) f(x) and g(x) by 0 for x = c. This doesn't change the limit since the limit doesn't depend on the value in the point (by definition).
According to Cauchy's mean value theorem there is a constant ξ in c < ξ < c + h such that:
Since f(c) = g(c) = 0,
If  then
then  and
and
With the indeterminate form infinity over infinity
The case when 
Let x < y < x + h. Then using Cauchy's mean value theorem:
We rewrite that in the form
and then by the discussion of the two cases
we show that the limit of f(x)/g(x) tends to the same when  and
and 
Other applications
Many other indeterminate forms, such as  ,
,  , and
, and 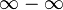 can be calculated using l'Hôpital's rule.
can be calculated using l'Hôpital's rule.
For example, to handle a case of 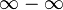 , the difference of two functions is converted to a quotient:
, the difference of two functions is converted to a quotient:
The rule can be used on indeterminate forms involving exponents by using logarithms to "move the exponent down."
Other methods of computing limits
Although l'Hôpital's rule is a powerful way of computing otherwise hard-to-compute limits, it is not always the easiest. Some limits are actually easier to compute using the Taylor series expansion.
For example,
Some elementary algebraic manipulation, however, yields:
And applying l'Hôpital's rule, we have:
On the other hand, a simple substitution also allows the use of l'Hôpital's rule.
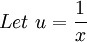 Therefore, as
Therefore, as 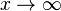 ,
, 
Therefore,
Logical circularity
In some cases it may constitute circular reasoning to use l'Hôpital's rule to evaluate such limits as
If one uses the evaluation of the limit above for the purpose of proving that
and one uses l'Hôpital's rule and the fact that
in the evaluation of the limit, the argument uses the expected proof to prove itself and is therefore fallacious (even though the conclusion of the proof happens to be true).
Another popular mistake of this nature is the well-known limit
Just as in the previous example, if one proves the differentiation rule for sin(x) with the limit, as is often the case in most calculus books, then it is circular to apply l'Hôpital's rule to evaluate the same limit.
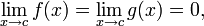
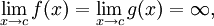



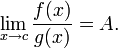
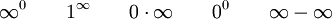



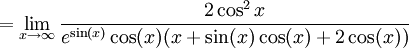


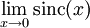

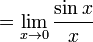

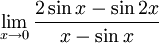



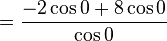
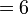
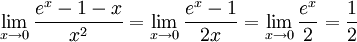
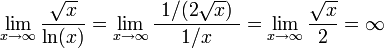
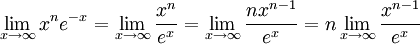


![\lim_{t\to 0}\, \mathrm{sinc}(f_0 t)\cdot \frac{\cos\left(\pi \alpha f_0 t\right)}{\left[1 - \left(2 \alpha f_0 t\right)^2\right]}](http://upload.wikimedia.org/math/f/0/d/f0dd7472ec51a1ee05d71e5929841532.png)
![= \left\{\lim_{t\to 0}\, \mathrm{sinc}(f_0 t)\right\}\cdot \left. \frac{\cos\left(\pi \alpha f_0 t\right)}{\left[1 - \left(2 \alpha f_0 t\right)^2\right]} \, \right|_{t = 0}](http://upload.wikimedia.org/math/d/1/a/d1a92e92c1e8df29f2df7a3374c6a162.png)

![\lim_{t\to \frac{1}{2\alpha f_0}} \mathrm{sinc}(f_0 t)\cdot \frac{\cos\left(\pi \alpha f_0 t\right)}{\left[1 - \left(2 \alpha f_0 t\right)^2\right]}](http://upload.wikimedia.org/math/c/c/6/cc6dd7fd51c402590ca4209e7901bea1.png)
![= \mathrm{sinc}\left(\frac{1}{2\alpha}\right)\cdot \lim_{t\to \frac{1}{2\alpha f_0}} \frac{\cos\left(\pi \alpha f_0 t\right)}{\left[1 - \left(2 \alpha f_0 t\right)^2\right]}](http://upload.wikimedia.org/math/9/b/b/9bbdeb2875e6cec7c70fb172d352bdd9.png)

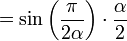




![\frac{f(x)}{g(x)} = \frac{f(y)}{g(x)} + \left [ 1 - \frac{g(y)}{g(x)} \right ] \frac{f'(\xi)}{g'(\xi)}](http://upload.wikimedia.org/math/4/b/2/4b2548d8cc3ac15edf419fb90d5b18cf.png)

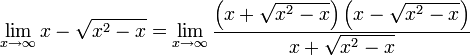
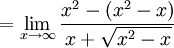





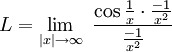

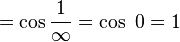
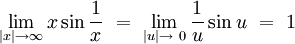

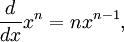

No comments:
Post a Comment