In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13... is an arithmetic progression with common difference 2.
If the initial term of an arithmetic progression is a1 and the common difference of successive members is d, then the nth term of the sequence is given by:
and in general
Sum (arithmetic series)
The sum of the components of an arithmetic progression is called an arithmetic series.
Calculating the value of an arithmetic series
The value of an arithmetic series consisting of n terms 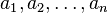 with delta d is given by
with delta d is given by
Intuitively, this formula can be derived by realizing that the sum of the first and last terms in the series is the same as the sum of the second and second to last terms, and so forth, and that there are roughly n / 2 such sums in the series. A version of this formula appears in the Liber Abaci (1202, ch. II.12) of Leonardo of Pisa (commonly known as Fibonacci). An often-told story is that Carl Friedrich Gauss rediscovered this formula when his third grade teacher asked the class to find the sum of the first 100 numbers, and he instantly computed the answer (5050).
A different way to get the result, that avoids the fuzziness of the previous method when the number of terms is odd, is to think in terms of averages. The value of the arithmetic series is the number of terms in the series times the average value of the terms. The average must be (a1 + an) / 2, since the values appear evenly spaced out around around this point on the real number line. Put another way,  is constant and equal to (a1 + an) / 2, which corresponds to the fact that successively taking terms from opposite sides of the series gives a constant average, which therefore must be the average of all terms in the series.
is constant and equal to (a1 + an) / 2, which corresponds to the fact that successively taking terms from opposite sides of the series gives a constant average, which therefore must be the average of all terms in the series.
Proof of the formula
Express the arithmetic series in two different ways:


Add both sides of the two equations. All terms involving d cancel, and so we're left with:

Rearranging and remembering that an = a1 + (n − 1)d, we get:
![S_n=\frac{n( a_1 + a_n)}{2}=\frac{n[ 2a_1 + (n-1)d]}{2}](http://upload.wikimedia.org/math/1/3/4/134fa4927dc3bef1cd63f89449590a13.png) .
.
Arithmetic series and sigma notation
Arithmetic series are commonly expressed using sigma notation. As an example, the arithmetic series

can be more succinctly written using sigma notation as

Likewise, an arithmetic series

can be written as

Product
The product of the components of an arithmetic progression with an initial element a1, common distance d, and n elements in total, is determined in a closed expression by
where  denotes the rising factorial and Γ denotes the Gamma function. (Note however that the formula is not valid when a1 / d is a negative integer or zero).
denotes the rising factorial and Γ denotes the Gamma function. (Note however that the formula is not valid when a1 / d is a negative integer or zero).
This is a generalization from the fact that the product of the progression 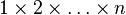 is given by the factorial n! and that the product
is given by the factorial n! and that the product
for positive integers m and n is given by
- infinite arithmetic series is an infinite series whose terms are in an arithmetic progression. Examples are 1 + 1 + 1 + 1 + · · · and 1 + 2 + 3 + 4 + · · ·. The general form for an infinite arithmetic series is


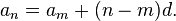
![S_n = a_1+a_2+\dots+a_n=\frac{n( a_1 + a_n)}{2} =\frac{n[ 2a_1 + (n-1)d ]}{2}.](http://upload.wikimedia.org/math/9/a/5/9a5fb55b3d24acaa271a9e4eea85cd83.png)
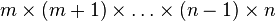

No comments:
Post a Comment