Mod,Floor, Nearest integer & Ceiling funtion

Mod Function:

The absolute value of a real number is denoted and defined as the "unsigned" portion of ,

			(1)
			(2)

where is the sign function. The absolute value is therefore always greater than or equal to 0. The absolute value of for real is plotted above.

he absolute value of a complex number , also called the complex modulus, is defined as

(3)

Note that the derivative (read: complex derivative) does not exist because at every point in the complex plane, the value of the derivative of depends on the direction in which the derivative is taken (so the Cauchy-Riemann equations cannot and do not hold). However, the real derivative (i.e., restricting the derivative to directions along the real axis) can be defined for points other than as

(4)

Floor Function:

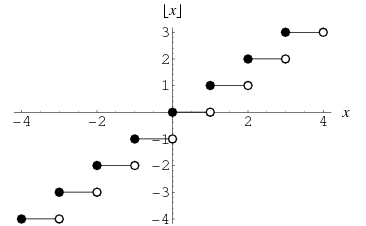
The floor function , also called the greatest integer function or integer value (Spanier and Oldham 1987), gives the largest integer less than or equal to . The name and symbol for the floor function were coined by K. E. Iverson (Graham et al. 1994).

Unfortunately, in many older and current works (e.g., Honsberger 1976, p. 30; Steinhaus 1999, p. 300; Shanks 1993; Ribenboim 1996; Hilbert and Cohn-Vossen 1999, p. 38; Hardy 1999, p. 18), the symbol is used instead of (Graham et al. 1990, p. 67). Because of the elegant symmetry of the floor function and ceiling function symbols and , and because is such a useful symbol when interpreted as an Iverson bracket, the use of to denote the floor function should be deprecated. In this work, the symbol is used to denote the nearest integer function since it naturally falls between the and symbols.

Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used (D. W. Cantrell, pers. comm.). Here, S&O indicates Spanier and Oldham (1987).

notation	name	S&O	Graham et al.	Mathematica
	ceiling function	--	ceiling, least integer	Ceiling[x]
	congruence	--	--	Mod[m, n]
	floor function		floor, greatest integer, integer part	Floor[x]
	fractional value		fractional part or	no name
	fractional part		no name	FractionalPart[x]
	integer part		no name	IntegerPart[x]
	nearest integer function	--	--	Round[x]
	quotient	--	--	Quotient[m, n]

The floor function satisfies the identity

(1)

for all integers .

A number of geometric-like sequences with a floor function in the numerator can be done analytically. For instance, sums of the form

(2)

can be done analytically for rational . For a unit fraction,

(3)

Sums of this form lead to Devil's staircase-like behavior.

For irrational 0" border="0" height="15" width="32">, continued fraction convergents , and ,

(4)

(Borwein et al. 2004, p. 12). This leads to the rather amazing result relating sums of the floor function of multiples of to the continued fraction of by

(5)

(Mahler 1929; Borwein et al. 2004, p. 12).

Nearest Integer Function:

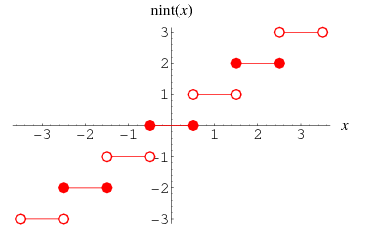
The nearest integer function nint(x) of , illustrated above and also called nint or the round function, is defined such that is the integer closest to . Since this definition is ambiguous for half-integers, the additional rule that half-integers are always rounded to even numbers is usually added in order to avoid statistical biasing. For example, , , , , etc. This convention is followed in the C math.h library function rint, as well as in Mathematica, where the nearest integer function is implemented as Round[x].

Although the notation is sometimes used to denote the nearest integer function (Hastad et al. 1988), this notation is rather cumbersome and is not recommended. Also note that while is used to denote the nearest integer function in this work, is also commonly used to denote the floor function .

Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used (D. W. Cantrell, pers. comm.). Here, S&O indicates Spanier and Oldham (1987).

notation	name	S&O	Graham et al.	Mathematica
	ceiling function	--	ceiling, least integer	Ceiling[x]
	congruence	--	--	Mod[m, n]
	floor function		floor, greatest integer, integer part	Floor[x]
	fractional value		fractional part or	no name
	fractional part		no name	FractionalPart[x]
	integer part		no name	IntegerPart[x]
	nearest integer function	--	--	Round[x]
	quotient	--	--	Quotient[m, n]

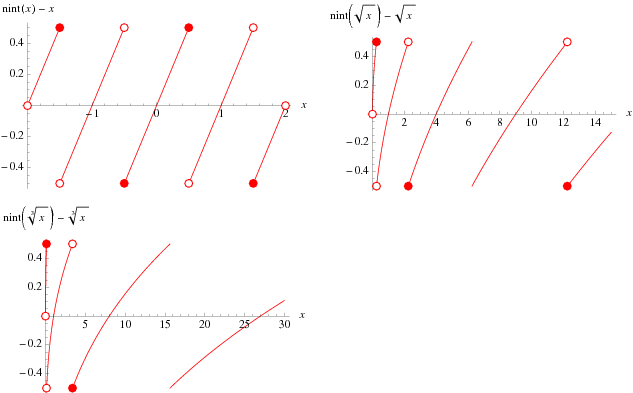
The plots above illustrate for small .

Ceiling Function:

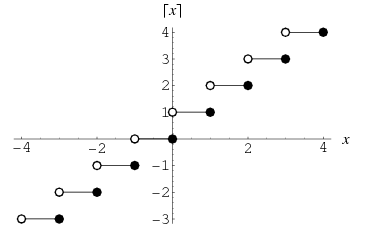
The function which gives the smallest integer =x" border="0" height="15" width="25">, shown as the thick curve in the above plot. Schroeder (1991) calls the ceiling function symbols the "gallows" because of the similarity in appearance to the structure used for hangings. The name and symbol for the ceiling function were coined by K. E. Iverson (Graham et al. 1990).

The ceiling function is implemented in Mathematica as Ceiling[z], where it is generalized to complex values of as illustrated above.

Although some authors used the symbol to denote the ceiling function (by analogy with the older notation for the floor function), this practice is strongly discouraged (Graham et al. 1990, p. 67). Also strongly discouraged is the use of the symbol to denote the ceiling function (e.g., Harary 1994, pp. 91, 93, and 118-119), since this same symbol is more commonly used to denote the fractional part of .

Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used (D. W. Cantrell, pers. comm.). Here, S&O indicates Spanier and Oldham (1987).

notation	name	S&O	Graham et al.	Mathematica
	ceiling function	--	ceiling, least integer	Ceiling[x]
	congruence	--	--	Mod[m, n]
	floor function		floor, greatest integer, integer part	Floor[x]
	fractional value		fractional part or	no name
	fractional part		no name	FractionalPart[x]
	integer part		no name	IntegerPart[x]
	nearest integer function	--	-	Round[x]
	quotient	--	--	Quotient[m, n]