Role as calculational tool
It is sometimes convenient to solve physical problems in a non-inertial reference frame. In such cases, it is necessary to introduce fictitious forces to account for the acceleration of the reference frame. For example, the surface of the Earth is a rotating reference frame. To solve classical mechanics problems exactly in an Earth-bound reference frame, two fictitious forces must be introduced, the Coriolis force and the centrifugal force (described below), of which the Coriolis force is dominant on Earth. Both of these fictitious forces are weak compared to most typical forces in everyday life, but they can be detected under careful conditions. For example, Léon Foucault was able to show the Coriolis force that results from the Earth's rotation using the Foucault pendulum. If the Earth were to rotate a thousandfold faster (making each day only ~86 seconds long), people could easily get the impression that such fictitious forces are pulling on them, as on a spinning carousel.
Detection of non-inertial reference frame
Philosophers[attribution needed] sometimes conjecture that a person living inside a closed box that is rotating (or otherwise accelerating) could not detect their own acceleration (rotation is a form of acceleration). That is not true, a person could not detect their velocity, but they could detect their acceleration (their change in velocity). Careful observers within the box can detect that they are in a non-inertial reference frame from the fictitious forces that arise from the acceleration of the box. They can even map out the magnitude and direction of the acceleration at every point within the box. The method by which this can be done is by detecting the movement of the box in a different rate/direction than their own for at least a short while.
This is similar to the lurch you would feel if you are driving and the driver suddenly speeds up: for a short while during and after the acceleration, the car is moving faster than you. Once your body catches up through the force of the seat pushing forward against your thigh or back, you stop feeling the lurch or shift (which is, in actuality, the force acting upon you). Another example of the detection of a non-inertial reference frame is the way a Foucault pendulum in a science museum will precess in exactly the same manner, regardless of whether the museum has walls or not.
In the box example, a person standing in the center of a very large box (for demonstration purposes, let's assume the box is large enough that they have some space around them and they're not touching a wall) has a velocity V, which is the same velocity of the box. If the box accelerated backwards rapidly, their feet would accelerate backwards with the box, faster than their body would accelerate, and they would trip forward. Although it might seem to those untrained in physics that a force had pushed him forward, that is an example of a fictitious force that relies on the movement of the box as a frame of reference (a frame of reference which is non-inertial). Someone with physics knowledge would probably be able to tell that the entire box had accelerated backwards, and their feet with it. A rule of thumb is that if you get lurched or turned in one direction, much like the man's feet were lurched backwards, it means the frame of reference you are in is accelerating in that direction.
Observers living inside a closed box that is moving uniformly (i.e., without acceleration) cannot detect their own motion. That is the essential physics of Newton's first two laws of motion.
Acceleration in a straight line
When a car accelerates hard, the common human response is to feel "pushed back into the seat." In an inertial frame of reference attached to the road, there is no physical force moving the rider backward. However, in the rider's non-inertial reference frame attached to the accelerating car, there is a backward fictitious force. We mention two possible ways of analyzing the problem:
- From the viewpoint of an inertial reference frame with constant velocity matching the initial motion of the car, the car is accelerating. In order for the passenger to stay inside the car, a force must be exerted on him. This force is exerted by the seat, which has started to move forward with the car and compressed against the passenger until it transmits the full force to keep the passenger inside. Thus the passenger is accelerating in this frame, due to the unbalanced force of the seat.
- From the point of view of the interior of the car, an accelerating reference frame, there is a fictitious force pushing the passenger backwards, with magnitude equal to the mass of the passenger times the acceleration of the car. This force pushes the passenger back into the seat, until the seat compresses and provides an equal and opposite force. Thereafter, the passenger is stationary in this frame, because the fictitious force and the (real) force of the seat are balanced.
This serves as an illustration of the manner in which fictitious forces arise from switching to a non-inertial reference frame. Calculations of physical quantities made in any frame give the same answers, but in some cases calculations are easier to make in a non-inertial frame. (In this simple example, the calculations are equally easy in either of the two frames described.)
Circular motion
A similar effect occurs in circular motion, circular for the standpoint of an inertial frame of reference attached to the road, with the fictitious force called the centrifugal force, fictitious when seen from a non-inertial frame of reference. If a car is moving at constant speed around a circular section of road, the occupants will feel pushed outside, away from the center of the turn. Again the situation can be viewed from inertial or non-inertial frames:
- From the viewpoint of an inertial reference frame stationary with respect to the road, the car is accelerating toward the center of the circle. This is called centripetal acceleration and requires a centripetal force to maintain the motion. This force is maintained by the friction of the wheels on the road. The car is accelerating, due to the unbalanced force, which causes it to move in a circle.
- From the viewpoint of a rotating frame, moving with the car, there is a fictitious centrifugal force that tends to push the car toward the outside of the road (and the occupants toward the outside of the car). The centrifugal force is balanced by the acceleration of the tires inward, making the car stationary in this non-inertial frame.
To consider another example, taking as our reference frame the surface of the rotating earth, centrifugal force reduces the apparent force of gravity by about one part in a thousand, depending on latitude. This is zero at the poles, maximum at the equator.
Another fictitious force that arises in the case of circular motion is the Coriolis force, which is ordinarily visible only in very large-scale motion like the projectile motion of long-range guns or the circulation of the earth's atmosphere. Neglecting air resistance, an object dropped from a 50 m high tower at the equator will fall 7.7 mm eastward of the spot below where it was dropped because of the Coriolis force.[2]
In the case of distant objects and a rotating reference frame, what must be taken into account is the resultant force of centrifugal and coriolis force. Consider a distant star observed from a rotating spacecraft. In the reference frame co-rotating with the spacecraft the distant star appears to move along a circular trajectory around the spacecraft. The apparent motion of the star is an apparent centripetal acceleration. Just like in the example above of the car in circular motion, the centrifugal force has the same magnitude as the fictitious centripetal force, but is directed in the opposite, centrifugal direction. In this case the coriolis force is twice the magnitude of the centrifugal force, and it points in centripetal direction. The vector sum of the centrifugal force and the coriolis force is the total fictitious force, which in this case points in centripetal direction.
Fictitious forces and work
Fictitious forces can be considered to do work, provided that they move an object on a trajectory that changes its energy from potential to kinetic. For example, consider a person in a rotating chair holding a weight in his outstretched arm. If he pulls his arm inward, from the perspective of his rotating reference frame he has done work against centrifugal force. If he now lets go of the weight, from his perspective it spontaneously flies outward, because centrifugal force has done work on the object, converting its potential energy into kinetic. From an inertial viewpoint, of course, the object flies away from him because it is suddenly allowed to move in a straight line. This illustrates that the work done, like the total potential and kinetic energy of an object, can be different in a non-inertial frame than an inertial one.
Gravity as a fictitious force
All fictitious forces are proportional to the mass of the object upon which they act, which is also true for gravity. This led Albert Einstein to wonder whether gravity was a fictitious force as well. He noted that a freefalling observer in a closed box would not be able to detect the force of gravity; hence, free falling reference frames are equivalent to an inertial reference frame (the equivalence principle). Following up on this insight, Einstein was able to show (after ~9 years of work) that gravity is indeed a fictitious force; the apparent acceleration is actually inertial motion in curved spacetime. This is the essential physics of Einstein's theory of general relativity.
Mathematical derivation of fictitious forces
General derivation
Consider a particle with mass m and position vector xa(t) in a particular inertial frame A. Consider a non-inertial frame B whose position relative to the inertial one is given by X(t). Since B is non-inertial, we must have that d2X/dt2 (the acceleration of frame B with respect to frame A) is non-zero. Let the position of the particle in frame B be xb(t). Then we have

Taking two time derivatives, this gives
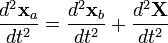
Now consider the forces in the problem. By Newton's Second Law, F = ma. The true force is of course the one in frame A (the inertial one), so

However, suppose we are working to solve a problem in frame B. It may be useful to consider the apparent force in this frame, which is given by

Now we define
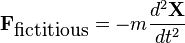
giving finally:
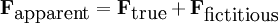
Thus we can solve problems in frame B by assuming that Newton's Second Law holds (with respect to quantities in that frame) and treating Ffictitious as an additional force.[3]
Rotating coordinate systems
A common situation in which noninertial reference frames are useful is when the reference frame is rotating. Since such rotational motion is non-inertial, due to the acceleration present in any rotational motion, a fictitious force can always be invoked by using a rotational frame of reference. Despite this complication, the use of fictitious forces often simplifies the calculations involved.
The relationship between acceleration in an inertial frame, and that in a coordinate frame rotating with angular velocity  can be expressed as
can be expressed as
where we have used the relationship for the time derivative of a vector in rotating coordinates
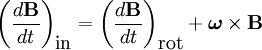 , for any vector
, for any vector 
Since  , the acceleration becomes
, the acceleration becomes
or, equivalently,
The acceleration in the rotating frame equals
Since the force in the rotating frame is  and, by definition,
and, by definition, 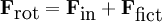 , the fictitious force equals
, the fictitious force equals
Here, the first term is the Coriolis force, the second term is the centrifugal force, and the third term is the Euler force.[4] When the rate of rotation doesn't change, as is typically the case for a planet, the Euler force is zero.
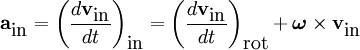




No comments:
Post a Comment