A dielectric, or electrical insulator, is a substance that is highly resistant to the flow of an electric current. Although a vacuum is also an excellent dielectric, the following discussion applies primarily to physical substances.
When a dielectric medium interacts with an applied electric field, charges are redistributed within its atoms or molecules. This redistribution alters the shape of an applied electrical field both inside the dielectric medium and in the region nearby.
When two electric charges move through a dielectric medium, the interaction energies and forces between them are reduced. When an electromagnetic wave travels through a dielectric, its speed decreases and its wavelength increases.
When an electric field is initially applied across a dielectric medium, a current flows. The total current flowing through a real dielectric is made up of two parts: a conduction and a displacement current. In good dielectrics, the conduction current will be extremely small. The displacement current can be considered the elastic response of the dielectric material to any change in the applied electric field. As the magnitude of the electric field is increased, a displacement current flows, and the additional displacement is stored as potential energy within the dielectric. When the electric field is decreased, the dielectric releases some of the stored energy as a displacement current. The electric displacement can be separated into a vacuum contribution and one arising from the dielectric by
where P is the polarization of the medium, E is the electric field, D is the electric flux density (or displacement), and χ its electric susceptibility. It follows that the relative permittivity and susceptibility of a dielectric are related, 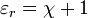 .
.
Dielectric constant
The dielectric constant is known to be measured by k, C=kCo is a measure of the extent to which a substance concentrates the electrostatic lines of flux. It is the ratio of the amount of electrical energy stored in an insulator, when a static electric field is imposed across it, relative to vacuum (which has a dielectric constant of 1). The dielectric constant is also known as the static permittivity.
Complex permittivity in dielectrics
Apart from a vacuum, the response of normal dielectrics to external fields generally depends on the frequency of the field. This frequency dependence is because a material's polarization does not respond instantaneously to an applied field. The response must always be causal (arising after the applied field). For this reason permittivity is often treated as a complex function of the frequency of the applied field ω, 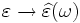 . The definition of permittivity therefore becomes
. The definition of permittivity therefore becomes
where D0 and E0 are the amplitudes of the displacement and electrical fields, respectively, i is the imaginary unit. The response of a medium to static electric fields is described by the low-frequency limit of permittivity, also called the static permittivity or dielectric constant  (also
(also  ):
):
At the high-frequency limit, the complex permittivity is commonly referred to as ε∞. At the plasma frequency and above, dielectrics behave as ideal metals, with electron gas behavior. The static permittivity is a good approximation for altering fields of low frequencies, and as the frequency increases a measurable phase difference δ emerges between D and E. The frequency at which the phase shift becomes noticeable depends on temperature and the details of the medium. For moderate fields strength (E0), D and E remain proportional, and
Since the response of materials to alternating fields is characterized by a complex permittivity, it is natural to separate its real and imaginary parts, which is done by convention in the following way:.
In the equation above, 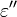 is the imaginary part of the permittivity, which is related to the rate at which energy is absorbed by the medium (converted into thermal energy, etcetera). The real part of the permittivity,
is the imaginary part of the permittivity, which is related to the rate at which energy is absorbed by the medium (converted into thermal energy, etcetera). The real part of the permittivity, 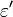 , is related to the refractive index of the medium.
, is related to the refractive index of the medium.
The study of capacitance involves using two key equations, they are Q=VC and W=0.5xQV
Dielectrics in Parallel-Plate Capacitors
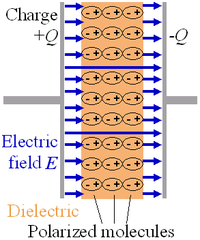
Putting a dielectric material between the plates in a parallel plate capacitor causes an increase in the capacitance in proportion to k, the relative permittivity of the material:
-
- where ε0 is the permittivity of free space, A is the area covered by the capacitors, and d is the distance between the plates.
This happens because an electric field polarizes the bound charges of the dielectric, producing concentrations of charge on its surfaces that create an electric field opposed (antiparallel) to that of the capacitor. Thus, a given amount of charge produces a weaker electric field between the plates than it would without the dielectric, which reduces the electric potential. Considered in reverse, this argument means that, with a dielectric, a given electric potential causes the capacitor to accumulate a larger charge polarization.
Applications
The use of a dielectric in a capacitor presents several advantages. The simplest of these is that the conducting plates can be placed very close to one another without risk of contact. Also, if subjected to a very high electric field, any substance will ionize and become a conductor. Dielectrics are more resistant to ionization than dry air, so a capacitor containing a dielectric can be subjected to a higher operating voltage. Layers of dielectric are commonly incorporated in manufactured capacitors to provide higher capacitance in a smaller space than capacitors using only air or a vacuum between their plates, and the term dielectric refers to this application as well as the insulation used in power and RF cables.
Some practical dielectrics
Dielectric materials can be solids, liquids, or gases. In addition, a high vacuum can also be a useful, lossless dielectric even though its relative dielectric constant is only unity.
Solid dielectrics are perhaps the most commonly used dielectrics in electrical engineering, and many solids are very good insulators. Some examples include porcelain, glass, and most plastics. Air, nitrogen and sulfur hexafluoride are the three most commonly used gaseous dielectrics.
- Industrial coatings such as parylene provide a dielectric barrier between the substrate and its environment.
- Mineral oil is used extensively inside electrical transformers as a fluid dielectric and to assist in cooling. Dielectric fluids with higher dielectric constants, such as electrical grade castor oil, are often used in high voltage capacitors to help prevent corona discharge and increase capacitance.
- Because dielectrics resist the flow of electricity, the surface of a dielectric may retain stranded excess electrical charges. This may occur accidentally when the dielectric is rubbed (the triboelectric effect). This can be useful, as in a Van de Graaff generator or electrophorus, or it can be potentially destructive as in the case of electrostatic discharge.
- Specially processed dielectrics, called electrets, may retain excess internal charge or "frozen in" polarization. Electrets have a semipermanent external electric field, and are the electrostatic equivalent to magnets. Electrets have numerous practical applications in the home and industry.
- Some dielectrics can generate a potential difference when subjected to mechanical stress, or change physical shape if an external voltage is applied across the material. This property is called piezoelectricity. Piezoelectric materials are another class of very useful dielectrics.
- Some ionic crystals and polymer dielectrics exhibit a spontaneous dipole moment which can be reversed by an externaly applied electric field. This behavior is called the ferroelectric effect. These materials are analogous to the way ferromagnetic materials behave within an externally applied magnetic field. Ferroelectric materials often have very high dielectric constants, making them quite useful for capacitors.
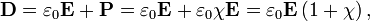

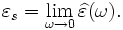
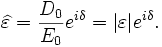
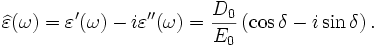
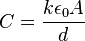
No comments:
Post a Comment