Newton's Laws of Motion

Newton's First Law

Newton's first law of motion – sometimes referred to as the "law of inertia."

Newton's first law of motion is often stated as:

An object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction ( provided there is no unbalanced force acting along that direction) .

There are two parts to this statement – one which predicts the behavior of stationary objects and the other which predicts the behaviour of moving objects. These two parts are summarized in the following diagram.

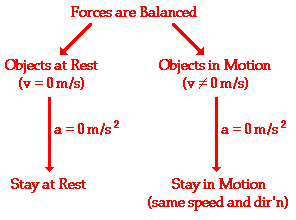
The behavior of all objects can be described by saying that objects tend to "keep on doing what they're doing" (provided there is no unbalanced force). If at rest, they will continue in this same state of rest. If in motion with an eastward velocity of 5 m/s, they will continue in this same state of motion (5 m/s, East). If in motion with a leftward velocity of 2 m/s, they will continue in this same state of motion (2 m/s, left). The state of motion of an object is maintained as long as the object is not acted upon by an unbalanced force. All objects resist changes in their state of motion – they tend to "keep on doing what they're doing."

There is a Pass the Water exercise that demonstrates this principle. If students participate in a relay race carrying a plastic container of water around a race track, the water will have a tendency to spill from the container at specific locations on the track. In general the water will spill when:

• the container is at rest and you attempt to move it
• the container is in motion and you attempt to stop it
• the container is moving in one direction and you attempt to change its direction.

The behavior of the water during the relay race can be explained by Newton's first law of motion. The water spills whenever the state of motion of the container changes. The water resists this change in its own state of motion and tends to "keep on doing what it is doing." If the container is moved from rest to a high speed at the starting line; the water remains at rest and spills onto the table. When the container stops near the finish line; the water keeps moving and spills over the container's leading edge. If the container is forced to move in a different direction to make it around a curve; the water keeps moving in the original direction and spills over its edge.

There are many applications of Newton's first law of motion. Consider some of your experiences in an automobile. Have you ever observed the behavior of coffee in a coffee cup filled to the rim while starting a car from rest or while bringing a car to rest from a state of motion? Coffee tends to "keep on doing what it is doing." When you accelerate a car from rest, the road provides an unbalanced force on the spinning wheels to push the car forward; yet the coffee (which is at rest) wants to stay at rest. While the car accelerates forward, the coffee remains in the same position; subsequently, the car accelerates out from under the coffee and the coffee spills in your lap. On the other hand, when braking from a state of motion the coffee continues to move forward with the same speed and in the same direction, ultimately hitting the wind shield or the dashboard. Coffee in motion tends to stay in motion.

Have you ever experienced inertia (resisting changes in your state of motion) in an automobile while it is braking to a stop? The force of the road on the locked wheels provides the unbalanced force to change the car's state of motion, yet there is no unbalanced force to change your own state of motion. Thus, you continue in motion, sliding forward along the seat. A person in motion tends to stay in motion with the same speed and in the same direction ... unless if unbalanced force acts. Yes, seat belts are used to provide safety for passengers whose motion is governed by Newton's laws. The seat belt provides the unbalanced force which brings you from a state of motion to a state of rest. Perhaps you could speculate what would occur when no seat belt is used.

There are many more applications of Newton's first law of motion. Several applications are listed below – try to provide explanations for each application.

• blood rushes from your head to your feet when riding on a descending elevator which suddenly stops.
• the head of a hammer can be tightened onto the wooden handle by banging the bottom of the handle against a hard surface.
• a brick is painlessly broken over the hand of a physics teacher by slamming the brick with a hammer. (CAUTION: Do not attempt this at home!)
• to dislodge ketchup from the bottom of a ketchup bottle, the bottle is often turned upside down, thrust downward at a high speed and then abruptly halted.
• headrests are placed in cars to prevent whiplash injuries during rear-end collisions.
• while riding a skateboard (or wagon or bicycle), you fly forward off the board when hitting a curb, a rock or another object which abruptly halts the motion of the skateboard.

Can you think of a few more examples which further illustrate applications of Newton's first law?

Newton's Second Law

Newton's first law of motion predicts the behavior of objects for which all existing forces are balanced. The first law – sometimes referred to as the "law of inertia" – states that if the forces acting upon an object are balanced, then the acceleration of that object will be 0 m/s². Objects at equilibrium (the condition in which all forces balance) will not accelerate. According to Newton, an object will only accelerate if there is a net or unbalanced force acting upon it. The presence of an unbalanced force will accelerate an object – changing its speed, its direction, or both its speed and direction.

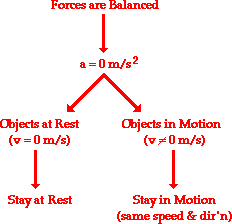
Newton's second law of motion pertains to the behavior of objects for which all existing forces are not balanced. The second law states that the acceleration of an object is dependent upon two variables – the net force acting upon the object and the mass of the object. The acceleration of an object depends directly upon the net force acting upon the object, and inversely upon the mass of the object. As the net force increases, so will the object's acceleration. However, as the mass of the object increases, its acceleration will decrease.

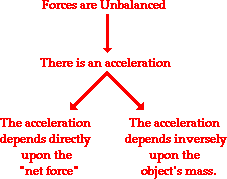
Newton's second law of motion can be formally stated as follows:

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

In terms of an equation, the net force is equal to the product of the object's mass and its acceleration.

F_net = m * a

Throughout this lesson, the emphasis has been on the "net force." The acceleration is directly proportional to the "net force;" the "net force" equals mass times acceleration; the acceleration is in the same direction as the "net force;" an acceleration is produced by a "net force." The NET FORCE. It is important to remember this distinction. Do not use the value of "any 'ole force" in the above equation; it is the net force, not any of the individual forces, which is related to acceleration. As discussed earlier, the net force is the vector sum of all the forces. If all the individual forces acting upon an object are known, then the net force can be determined. If necessary, review this principle by returning to the practice questions in Lesson 2.

The above equation also indicates that a unit of force is equal to a unit of mass multiplied by a unit of acceleration. By substituting standard metric units for force, mass, and acceleration into the above equation, the following unit equivalency can be written:

Thus, the definition of the standard metric unit of force is given by the above equation.

One Newton is defined as the amount of force required to give a 1-kg mass an acceleration of 1 m/s².

The net force equation (F_net = m * a) can also be used as a "recipe" for algebraic problem-solving. The table below can be filled by substituting the known variables into the equation, then solving for the unknown quantity. Try it by yourself and then use the pop-up menus to view the answers.

	Net Force (N)	Mass (kg)	Acceleration (m/s2)
1.	10	2	Depress mouse. a = 5 m/s/s a = F/m a = 10 N/2 kg a = 5 m/s/s
2.	20	2	Depress mouse. a = 10 m/s/s a = F/m a = 20 N/2 kg a = 10 m/s/s
3.	20	4	Depress mouse. a = 5 m/s/s a = F/m a = 20 N/4 kg a = 5 m/s/s
4.	Depress mouse. F = 10 N F = m a F = 2 kg x 5 m/s/s F = 10 N	2	5
5.	10	Depress mouse. m = 1 kg m = F/a m = 10 N/10 m/s/s m = 1 kg	10

The numerical information in the table above demonstrates the important qualitative relationships between force, mass, and acceleration.

Comparing the values in rows 1 and 2, you see that doubling the net force results in a doubling of the acceleration (if mass is held constant). Similarly, comparing the values in rows 2 and 4 demonstrates that "halving" the net force results in a "halving" of the acceleration (if mass is held constant). Acceleration is directly proportional to net force.

Observe from rows 2 and 3 that doubling the mass results in a "halving" of the acceleration (if force is held constant). And similarly, rows 4 and 5 show that "halving" the mass results in a doubling of the acceleration (if force is held constant). Acceleration is inversely proportional to mass.

Analysis of the data in the table illustrates that an equation such as F_net = m*a can used as a guide when thinking about how a variation in one quantity might affect another quantity. Whatever change is made of the net force, the same change will occur in the acceleration. Double, triple or quadruple the net force, and the acceleration will do the same. On the other hand, whatever change is made of the mass, the opposite or inverse change will occur in the acceleration. Double, triple or quadruple the mass, and the acceleration will be one-half, one-third or one-fourth of its original value.

As stated above, the direction of the net force is the same as the direction of the acceleration. Thus, if the direction of the acceleration is known, then so is the direction of the net force.

Consider the two ticker tape traces below which represent the acceleration of a car. From the traces, determine the direction of the net force upon the car. Then depress the mouse on the pop-up menus to view the answer. (Review acceleration.)

Depress mouse for answer. The net force is to the right since the acceleration is to the right. An object which moves to the right and speeds up has a rightward acceleration.
Depress mouse for answer. The net force is to the left since the acceleration is to the left. An object which moves to the right and slows down has a leftward acceleration.

In conclusion, Newton's second law explains the behavior of objects upon which unbalanced forces are acting. The law states that unbalanced forces cause objects to accelerate with an acceleration that is directly proportional to the net force and inversely proportional to the mass of the object.

Check Your Understanding

1. What acceleration will result when a 12-N net force is applied to a 3-kg object? A 6-kg object?

Depress mouse to view answer. A 3-kg object experiences an accel'n of 4 m/s/s. A 6-kg object experiences an accel'n of 2 m/s/s.

2. A net force of 16 N causes a mass to accelerate at the rate of 5 m/s². Determine the mass.

Depress mouse to view answer. Use Fnet=m*a with Fnet=16 N and a=5 m/s/s. So (16 N) = (m)*(5 m/s/s) And m = 3.2 kg

3. An object is accelerating at 2 m/s². If the net force is tripled and the mass of the object is doubled, what is the new acceleration?

Depress mouse to view answer. Answer: 3 m/s/s. The original accel'n of 2 m/s/s must be multiplied by 3 (since a and F are directly proportional) and divided by 2 (since a and m are inversely proportional).

4. An object is accelerating at 2 m/s². If the net force is tripled and the mass of the object is halved, what is the new acceleration?

Depress mouse to view answer. Answer: 12 m/s/s. The original accel'n of 2 m/s/s must be multiplied by 3 (since a and F are directly proportional) and divided by 1/2 (since a and m are inversely proportional).

---

Newton's Third Law

A force is a push or a pull upon an object which results from its interaction with another object. Forces result from interactions! Some forces result from contact interactions (normal, frictional, tensional, and applied forces are examples of contact forces) and other forces result from action-at-a-distance interactions (gravitational, electrical, and magnetic forces are examples of action-at-a-distance forces). According to Newton, whenever objects A and B interact with each other, they exert forces upon each other. When you sit in your chair, your body exerts a downward force on the chair and the chair exerts an upward force on your body. There are two forces resulting from this interaction — a force on the chair and a force on your body. These two forces are called action and reaction forces and are the subject of Newton's third law of motion. Formally stated, Newton's third law is:

"For every action, there is an equal and opposite reaction."

The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the force on the first object equals the size of the force on the second object. The direction of the force on the first object is opposite to the direction of the force on the second object. Forces always come in pairs – equal and opposite action-reaction force pairs.

A variety of action-reaction force pairs are evident in nature. Consider the propulsion of a fish through the water. A fish uses its fins to push water backwards. But a push on the water will only serve to accelerate the water. In turn, the water reacts by pushing the fish forwards, propelling the fish through the water. The size of the force on the water equals the size of the force on the fish; the direction of the force on the water (backwards) is opposite to the direction of the force on the fish (forwards). For every action, there is an equal (in size) and opposite (in direction) reaction force. Action-reaction force pairs make it possible for fishes to swim.

Consider the flying motion of birds. A bird flies by use of its wings. The wings of a bird push air downwards. In turn, the air reacts by pushing the bird upwards. The size of the force on the air equals the size of the force on the bird; the direction of the force on the air (downwards) is opposite to the direction of the force on the bird (upwards). For every action, there is an equal (in size) and opposite (in direction) reaction. Action-reaction force pairs make it possible for birds to fly.

Consider the motion of your automobile on your way to school. An automobile is equipped with wheels that spin backwards. As the wheels spin backwards, they push the road backwards. In turn, the road reacts by pushing the wheels forward. The size of the force on the road equals the size of the force on the wheels (or automobile); the direction of the force on the road (backwards) is opposite to the direction of the force on the wheels (forwards). For every action, there is an equal (in size) and opposite (in direction) reaction. Action-reaction force pairs make it possible for automobiles to move.

Check Your Understanding

1. While driving, Anna Litical observed a bug striking the windshield of her car. Obviously, a case of Newton's third law of motion. The bug hit the windshield and the windshield hit the bug. Which of the two forces is greater: the force on the bug or the force on the windshield?

Depress mouse to see answer. Trick Question! The forces are equal in size. For every action, there is an equal ... (equal!) reaction. The fact that the bug splatters only means that with its smaller mass, it is less able to withstand the larger acceleration resulting from the interaction.

2. Rockets are unable to accelerate in space because ...

1. there is no air in space for the rockets to push off of.
2. there is no gravity is in space.
3. there is no air resistance in space.
4. ... nonsense! Rockets do accelerate in space.

Depress mouse to see answer. The answer is D. It is a common misconception that rockets are unable to accelerate in space. Rockets do accelerate in space. Rockets are able to accelerate due to the fact that they burn fuel and push the exhaust gases in a direction opposite to the direction in which they wish to accelerate.

3. A gun recoils when it is fired. The recoil is the result of action-reaction force pairs. As the gases from the gunpowder explosion expand, the gun pushes the bullet forwards and the bullet pushes the gun backwards. The acceleration of the recoiling gun is ...

1. greater than the acceleration of the bullet.
2. smaller than the acceleration of the bullet.
3. the same size as the acceleration of the bullet.

Depress mouse to see answer. The answer is B. The force on the gun equals the force on the bullet. However, acceleration depends on both force and mass. The bullet has a greater acceleration due to the fact that it has a smaller mass. Remember: acceleration and mass are inversely proportional.

4. In the top picture, a physics student is pulling upon a rope which is attached to a wall. In the bottom picture, the physics student is pulling upon a rope which is held by the Strongman. In each case, the force scale reads 500 Newtons. The physics student is pulling

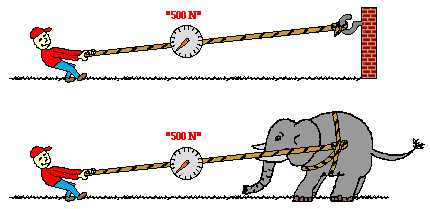
1. with more force when the rope is attached to the wall.
2. with more force when the rope is attached to the Strongman.
3. the same force in each case.

Depress mouse to see answer. The answer is C. The student is pulling with 500 N of force in each case. The rope transmits the force from the physics student to the wall (or to the Strongman) and vice versa. Since the force of the student pulling on the wall and the wall pulling on the student are action-reaction force pairs, they must have equal magnitudes. Inanimate objects such as walls can also push and pull.

---