Friction is the force that opposes the relative motion or tendency toward such motion of two surfaces in contact. It is not a fundamental force, as it is made up of electromagnetic forces between atoms. When contacting surfaces move relative to each other, the friction between the two objects converts kinetic energy into thermal energy, or heat. Friction between solid objects and fluids (gases or liquids) is called drag. Friction in an electronic circuit is called resistance. Contrary to popular belief, sliding friction is not caused by surface roughness, but by chemical bonding between the surfaces - by the stickiness of the two surfaces.
Classical approximation
The classical approximation of the force of friction between two solid surfaces is known as Coulomb friction, named after Charles-Augustin de Coulomb. The equation is:
 ,
,
where-
- μ is the coefficient of friction, which is an empirical property of the contacting materials,
- N is the normal force exerted between the surfaces, and
- Ff is either the force exerted by friction, or, in the case of equality, the maximum possible magnitude of this force.
For surfaces in relative motion, μ is the coefficient of kinetic friction (see below), the Coulomb friction is equal to Ff, and the frictional force on each surface is exerted in the direction opposite to its motion relative to the other surface.
For surfaces at rest relative to each other, μ is the coefficient of static friction (generally larger than its kinetic counterpart), the Coulomb friction may take any value from zero up to Ff, and the direction of the frictional force on a surface is opposite to the motion that surface would experience in the absence of friction. Thus, in the static case, the frictional force is exactly what it must be in order to prevent motion between the surfaces; it balances the net force tending to cause such motion. In this case, rather than providing an estimate of the actual frictional force, the Coulomb approximation provides a threshold value for this force, above which sliding would commence.
This approximation mathematically follows from the assumptions that surfaces are in atomically close contact only over a small fraction of their overall area, that this contact area is proportional to the normal force (until saturation, which takes place when all area is in atomic contact), and that frictional force is proportional to contact area. Such reasoning aside, however, the approximation is fundamentally an empirical construction. Rather than a physical law, it is a rule of thumb describing the approximate outcome of an extremely complicated physical interaction. The strength of the approximation is its simplicity and versatility--though in general the relationship between normal force and frictional force is not exactly linear (and so the frictional force is not entirely independent of the contact area of the surfaces), the Coulomb approximation is an adequate representation of friction for the analysis of many physical systems.
The coefficient of friction (also known as the frictional coefficient) is a dimensionless scalar value which describes the ratio of the force of friction between two bodies and the force pressing them together. The coefficient of friction depends on the materials used -- for example, ice on steel has a low coefficient of friction (the two materials slide past each other easily), while rubber on pavement has a high coefficient of friction (the materials do not slide past each other easily). Coefficients of friction range from near zero to greater than one - under good conditions, a tire on concrete may have a coefficient of friction of 1.7.
When the surfaces are adhesive, Coulomb friction becomes a very poor approximation (for example, Scotch tape resists sliding even when there is no normal force, or a negative normal force). In this case, the frictional force may depend strongly on the area of contact. Some drag racing tires are adhesive in this way.
The force of friction is always exerted in a direction that opposes movement (for kinetic friction) or potential movement (for static friction) between the two surfaces. For example, a curling stone sliding along the ice experiences a kinetic force slowing it down. For an example of potential movement, the drive wheels of an accelerating car experience a frictional force pointing forward; if they did not, the wheels would spin, and the rubber would slide backwards along the pavement. Note that it is not the direction of movement of the vehicle they oppose, it is the direction of (potential) sliding between tire and road.
The coefficient of friction is an empirical measurement -- it has to be measured experimentally, and cannot be found through calculations. Rougher surfaces tend to have higher values. Most dry materials in combination have friction coefficient values between 0.3 and 0.6. Values outside this range are rarer, but Teflon, for example, can have a coefficient as low as 0.04. A value of zero would mean no friction at all, an elusive property--even Magnetic levitation vehicles have drag. Rubber in contact with other surfaces can yield friction coefficients from 1.0 to 2.
Static friction
Static friction occurs when the two objects are not moving relative to each other (like a rock on a table). The coefficient of static friction is typically denoted as μs. The initial force to get an object moving is often dominated by static friction. The static friction is in most cases higher than the kinetic friction. Rolling friction occurs when one object "rolls" on another (like a car's wheels on the ground). This is classified under static friction because the patch of the tire in contact with the ground, at any point while the tire spins, is stationary relative to the ground. The coefficient of rolling friction is typically denoted as μr.
Limiting friction is the maximum value of static friction, or the force of friction that acts when a body is just on the verge of motion on a surface.
Kinetic friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground). The coefficient of kinetic friction is typically denoted as μk, and is usually less than the coefficient of static friction. From the mathematical point of view, however, the difference between static and kinetic friction is of minor importance: Let us have a coefficient of friction which depends on the sliding velocity and is such that its value at 0 (the static friction μs ) is the limit of the kinetic friction μk for the velocity tending to zero. Then a solution of the contact problem with such Coulomb friction solves also the problem with the original μk and any static friction greater than that limit.
Since friction is exerted in a direction that opposes movement, kinetic friction usually does negative work, typically slowing something down. There are exceptions however, if the surface itself is under acceleration. One can see this by placing a heavy box on a rug, then pulling on the rug quickly. In this case, the box slides backwards relative to the rug, but moves forward relative to the floor. Thus, the kinetic friction between the box and rug accelerates the box in the same direction that the box moves, doing positive work.
Examples of kinetic friction:
- Sliding friction is when two objects are rubbing against each other. Putting a book flat on a desk and moving it around is an example of sliding friction
- Fluid friction is the friction between a solid object as it moves through a liquid or a gas. The drag of air on an airplane or of water on a swimmer are two examples of fluid friction.
- Resistance is the atomic friction of an electronic circuit or device as an electric current flows through it.
Reducing friction
Devices
Devices such as tires, ball bearings or rollers can change sliding friction into a much smaller type of rolling friction. Many thermoplastic materials such as nylon, HDPE and PTFE are commonly used for low friction bearings. They are especially useful because the coefficient of friction falls with increasing imposed load.
Techniques
One technique used by railroad engineers is to back up the train to create slack in the linkages between cars. This allows the train engine to pull forward and only take on the static friction of one car at a time, instead of all cars at once, thus spreading the static frictional force out over time.
Lubricants
A common way to reduce friction is by using a lubricant, such as oil, water, or grease, which is placed between the two surfaces, often dramatically lessening the coefficient of friction. The science of friction and lubrication is called tribology. Lubricant technology is when lubricants are mixed with the application of science, especially to industrial or commercial objectives.
Superlubricity, a recently-discovered effect, has been observed in graphite: it is the substantial decrease of friction between two sliding objects, approaching zero levels (a very small amount of frictional energy would still be dissipated).
Lubricants to overcome friction need not always be thin, turbulent fluids or powdery solids such as graphite and talc; acoustic lubrication actually uses sound as a lubricant.
Energy of friction
According to the law of conservation of energy, no energy is destroyed due to friction, though it may be lost to the system of concern. Energy is transformed from other forms into heat. A sliding hockey puck comes to rest due to friction as its kinetic energy changes into heat. Since heat quickly dissipates, many early philosophers, including Aristotle, wrongly concluded that moving objects lose energy without a driving force.
When an object is pushed along a surface, the energy converted to heat is given by:

-
- where
- N is the normal force,
- μk is the coefficient of kinetic friction,
- x is the coordinate along which the object transverses.
- where
-
Physical deformation is associated with friction. While this can be beneficial, as in polishing, it is often a problem, as the materials are worn away, and may no longer hold the specified tolerances.
The work done by friction can translate into deformation and heat that in the long run may affect the surface's specification and the coefficient of friction itself. Friction can in some cases cause solid materials to melt.
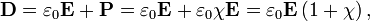
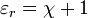 .
.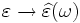 . The definition of permittivity therefore becomes
. The definition of permittivity therefore becomes
 (also
(also  ):
):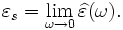
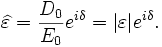
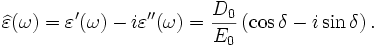
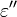 is the imaginary part of the permittivity, which is related to the rate at which energy is absorbed by the medium (converted into thermal energy, etcetera). The real part of the permittivity,
is the imaginary part of the permittivity, which is related to the rate at which energy is absorbed by the medium (converted into thermal energy, etcetera). The real part of the permittivity, 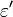 , is related to the
, is related to the 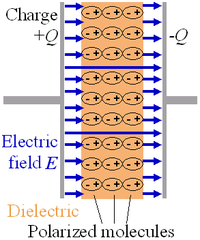
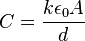

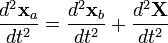


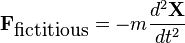
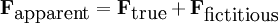
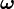 can be expressed as
can be expressed as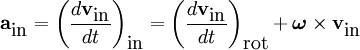
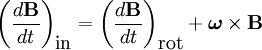 , for any vector
, for any vector 
 , the acceleration becomes
, the acceleration becomes


 and, by definition,
and, by definition,  , the fictitious force equals
, the fictitious force equals
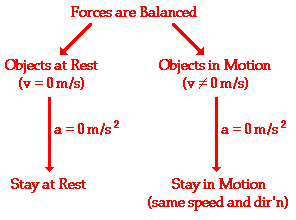


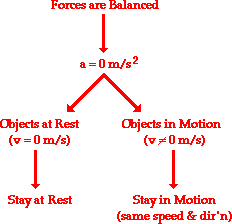
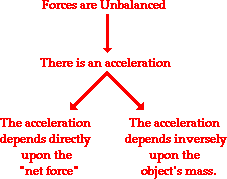
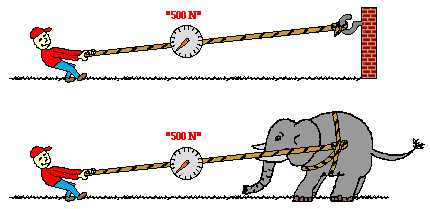
 In terms of an equation, the net force is equal to the product of the object's mass and its acceleration.
In terms of an equation, the net force is equal to the product of the object's mass and its acceleration. A force is a push or a pull upon an object which results from its interaction with another object. Forces result from interactions! Some forces result from contact interactions (normal, frictional, tensional, and applied forces are examples of contact forces) and other forces result from action-at-a-distance interactions (gravitational, electrical, and magnetic forces are examples of action-at-a-distance forces). According to Newton, whenever objects A and B interact with each other, they exert forces upon each other. When you sit in your chair, your body exerts a downward force on the chair and the chair exerts an upward force on your body. There are two forces resulting from this interaction — a force on the chair and a force on your body. These two forces are called action and reaction forces and are the subject of Newton's third law of motion. Formally stated, Newton's third law is:
A force is a push or a pull upon an object which results from its interaction with another object. Forces result from interactions! Some forces result from contact interactions (normal, frictional, tensional, and applied forces are examples of contact forces) and other forces result from action-at-a-distance interactions (gravitational, electrical, and magnetic forces are examples of action-at-a-distance forces). According to Newton, whenever objects A and B interact with each other, they exert forces upon each other. When you sit in your chair, your body exerts a downward force on the chair and the chair exerts an upward force on your body. There are two forces resulting from this interaction — a force on the chair and a force on your body. These two forces are called action and reaction forces and are the subject of Newton's third law of motion. Formally stated, Newton's third law is: