Viscosity is a measure of the resistance of a fluid to deform under shear stress. It is commonly perceived as "thickness", or resistance to flow. Viscosity describes a fluid's internal resistance to flow and may be thought of as a measure of fluid friction. Thus, water is "thin", having a lower viscosity, while vegetable oil is "thick" having a higher viscosity. All real fluids (except superfluids) have some resistance to shear stress, but a fluid which has no resistance to shear stress is known as an ideal fluid or inviscid fluid (Symon 1971).
When looking at a value for viscosity the number that one most often sees is the coefficient of viscosity, simply put this is the ratio between the pressure exerted on the surface of a fluid, in the lateral or horizontal direction, to the change in velocity of the fluid as you move down in the fluid (this is what is referred to as a velocity gradient). For example, at "room temperature", water has a nominal viscosity of 1.0 x 10
-3 Pa∙s and motor oil has a nominal apparent viscosity of 250 x 10
-3 Pa∙s.
The word "viscosity" derives from the
Latin word "
viscum" for
mistletoe. A viscous glue was made from mistletoe berries and used for lime-twigs to catch birds.
Newton's theory

Laminar shear of fluid between two plates. Friction between the fluid and the moving boundaries causes the fluid to shear. The force required for this action is a measure of the fluid's viscosity. This type of flow is known as a
Couette flow.

Laminar shear, the non-linear gradient, is a result of the geometry the fluid is flowing through (e.g. a pipe).
In general, in any flow, layers move at different velocities and the fluid's viscosity arises from the shear stress between the layers that ultimately opposes any applied force.
Isaac Newton postulated that, for straight, parallel and uniform flow, the shear stress, τ, between layers is proportional to the velocity gradient, ∂u/∂y, in the direction perpendicular to the layers, in other words, the relative motion of the layers.
 .
.
Here, the constant η is known as the coefficient of viscosity, the viscosity, or the dynamic viscosity. Many fluids, such as water and most gases, satisfy Newton's criterion and are known as Newtonian fluids. Non-Newtonian fluids exhibit a more complicated relationship between shear stress and velocity gradient than simple linearity.
The relationship between the shear stress and the velocity gradient can also be obtained by considering two plates closely spaced apart at a distance y, and separated by a homogeneous substance. Assuming that the plates are very large, with a large area A, such that edge effects may be ignored, and that the lower plate is fixed, let a force F be applied to the upper plate. If this force causes the substance between the plates to undergo shear flow (as opposed to just shearing elastically until the shear stress in the substance balances the applied force), the substance is called a fluid. The applied force is proportional to the area and velocity of the plate and inversely proportional to the distance between the plates. Combining these three relations results in the equation F = η(Au/y), where η is the proportionality factor called the absolute viscosity (with units Pa·s = kg/(m·s) or slugs/(ft·s)). The absolute viscosity is also known as the dynamic viscosity, and is often shortened to simply viscosity. The equation can be expressed in terms of shear stress; τ = F/A = η(u/y). The rate of shear deformation is u / y and can be also written as a shear velocity, du/dy. Hence, through this method, the relation between the shear stress and the velocity gradient can be obtained.
In many situations, we are concerned with the ratio of the viscous force to the inertial force, the latter characterised by the fluid density ρ. This ratio is characterised by the kinematic viscosity, defined as follows:
 .
.
James Clerk Maxwell called viscosity fugitive elasticity because of the analogy that elastic deformation opposes shear stress in solids, while in viscous fluids, shear stress is opposed by rate of deformation.
Measuring viscosity
Viscosity is measured with various types of viscometer. Close temperature control of the fluid is essential to accurate measurements, particularly in materials like lubricants, whose viscosity (-40 <>
For some fluids, it is a constant over a wide range of shear rates. The fluids without a constant viscosity are called Non-Newtonian fluids.
In paint industries, viscosity is commonly measured with a Zahn cup, in which the efflux time is determined and given to customers. The efflux time can also be converted to kinematic viscosities (cSt) through the conversion equations.
Also used in paint, a Stormer viscometer uses load-based rotation in order to determine viscosity. It uses units, Krebs units (KU), unique to this viscometer.
Units
Viscosity (dynamic/absolute viscosity): η or μ
The IUPAC symbol for viscosity is the Greek symbol eta (η), and dynamic viscosity is also commonly referred to using the Greek symbol mu (μ). The SI physical unit of dynamic viscosity is the pascal-second (Pa·s), which is identical to 1 kg·m−1·s−1. If a fluid with a viscosity of one Pa·s is placed between two plates, and one plate is pushed sideways with a shear stress of one pascal, it moves a distance equal to the thickness of the layer between the plates in one second. The name poiseuille (Pl) was proposed for this unit (after Jean Louis Marie Poiseuille who formulated Poiseuille's law of viscous flow), but not accepted internationally. Care must be taken in not confusing the poiseuille with the poise named after the same person!
The cgs physical unit for dynamic viscosity is the poise[1] (P; IPA: [pwaz])) named after Jean Louis Marie Poiseuille. It is more commonly expressed, particularly in ASTM standards, as centipoise (cP). The centipoise is commonly used because water has a viscosity of 1.0020 cP (at 20 °C; the closeness to one is a convenient coincidence).
- 1 P = 1 g·cm−1·s−1
The relation between Poise and Pascal-second is:
- 10 P = 1 kg·m−1·s−1 = 1 Pa·s
- 1 cP = 0.001 Pa·s = 1 mPa·s
Kinematic viscosity: ν
Kinematic viscosity (Greek symbol: ν) has SI units (m2·s−1). The cgs physical unit for kinematic viscosity is the stokes (abbreviated S or St), named after George Gabriel Stokes. It is sometimes expressed in terms of centistokes (cS or cSt). In U.S. usage, stoke is sometimes used as the singular form.
- 1 stokes = 100 centistokes = 1 cm2·s−1 = 0.0001 m2·s−1.
- 1 centistokes = 1 mm²/s
Dynamic versus kinematic viscosity
Conversion between kinematic and dynamic viscosity, is given by νρ = η. Note that the parameters must be given in SI units not in P, cP or St.
For example, if ν = 1 St (=0.0001 m2·s-1) and ρ = 1000 kg m-3 then η = νρ = 0.1 kg·m−1·s−1 = 0.1 Pa·s [1].
For a plot of kinematic viscosity of air as a function of absolute temperature, see James Ierardi's Fire Protection Engineering Site
Molecular origins

Pitch has a viscosity approximately 100 billion times that of water.
The viscosity of a system is determined by how molecules constituting the system interact. There are no simple but correct expressions for the viscosity of a fluid. The simplest exact expressions are the Green-Kubo relations for the linear shear viscosity or the Transient Time Correlation Function expressions derived by Evans and Morriss in 1985. Although these expressions are each exact in order to calculate the viscosity of a dense fluid, using these relations requires the use of molecular dynamics computer simulation.
Gases
Viscosity in gases arises principally from the molecular diffusion that transports momentum between layers of flow. The kinetic theory of gases allows accurate prediction of the behaviour of gaseous viscosity, in particular that, within the regime where the theory is applicable:
- Viscosity is independent of pressure; and
- Viscosity increases as temperature increases.
Liquids
In liquids, the additional forces between molecules become important. This leads to an additional contribution to the shear stress though the exact mechanics of this are still controversial.[citation needed] Thus, in liquids:
- Viscosity is independent of pressure (except at very high pressure); and
- Viscosity tends to fall as temperature increases (for example, water viscosity goes from 1.79 cP to 0.28 cP in the temperature range from 0 °C to 100 °C); see temperature dependence of liquid viscosity for more details.
The dynamic viscosities of liquids are typically several orders of magnitude higher than dynamic viscosities of gases.
Viscosity of materials
The viscosity of air and water are by far the two most important materials for aviation aerodynamics and shipping fluid dynamics. Temperature plays the main role in determining viscosity.
Viscosity of air
The viscosity of air depends mostly on the temperature. At 15.0 °C, the viscosity of air is 1.78 × 10−5 kg/(m·s). You can get the viscosity of air as a function of altitude from the eXtreme High Altitude Calculator
Viscosity of water
The viscosity of water is 8.90 × 10-4 Pa·s or 8.90 × 10-3 dyn·s/cm2at about 25 °C.
as a function of temperature: μ=A × 10B/(T-C)
Where A=2.414 × 10-5 N*s/m2 ; B = 247.8 Kelvin ; C = 140 Kelvin
Viscosity of various materials

Example of the viscosity of milk and water. Liquids with higher viscosities will not make such a splash when poured at the same velocity.
The Sutherland's formula can be used to derive the dynamic viscosity as a function of the temperature:

where:
- η = viscosity in (Pa·s) at input temperature T
- η0 = reference viscosity in (Pa·s) at reference temperature T0
- T = input temperature in kelvin
- T0 = reference temperature in kelvin
- C = Sutherland's constant
Valid for temperatures between 0 < T <>
Sutherland's constant and reference temperature for some gases
Some dynamic viscosities of Newtonian fluids are listed below:
Gases (at 0 °C):
Liquids (at 25 °C):
a Data from CRC Handbook of Chemistry and Physics, 73rd edition, 1992-1993.
Fluids with variable compositions, such as honey, can have a wide range of viscosities.
A more complete table can be found here, including the following:
| viscosity [cP] |
| honey | 2,000–10,000 |
| molasses | 5,000–10,000 |
| molten glass | 10,000–1,000,000 |
| chocolate syrup | 10,000–25,000 |
| chocolate* | 45,000–130,000 [2] |
| ketchup* | 50,000–100,000 |
| peanut butter | ~250,000 |
| shortening* | ~250,000 |
* These materials are highly non-Newtonian.
Can solids have a viscosity?
If on the basis that all solids flow to a small extent in response to shear stress then yes, substances known as Amorphous solids, such as glass, may be considered to have viscosity. This has led some to the view that solids are simply liquids with a very high viscosity, typically greater than 1012 Pa•s. This position is often adopted by supporters of the widely held misconception that glass flow can be observed in old buildings. This distortion is more likely the result of glass making process rather than the viscosity of glass.
However, others argue that solids are, in general, elastic for small stresses while fluids are not. Even if solids flow at higher stresses, they are characterized by their low-stress behavior. Viscosity may be an appropriate characteristic for solids in a plastic regime. The situation becomes somewhat confused as the term viscosity is sometimes used for solid materials, for example Maxwell materials, to describe the relationship between stress and the rate of change of strain, rather than rate of shear.
These distinctions may be largely resolved by considering the constitutive equations of the material in question, which take into account both its viscous and elastic behaviors. Materials for which both their viscosity and their elasticity are important in a particular range of deformation and deformation rate are called viscoelastic. In geology, earth materials that exhibit viscous deformation at least three times greater than their elastic deformation are sometimes called rheids.
One example of solids flowing which has been observed since 1930 is the Pitch drop experiment.
Bulk viscosity
The trace of the stress tensor is often identified with the negative-one-third of the thermodynamic pressure,
 ,
,
which only depends upon the equilibrium state potentials like temperature and density (equation of state). In general, the trace of the stress tensor is the sum of thermodynamic pressure contribution plus another contribution which is proportional to the divergence of the velocity field. This constant of proportionality is called the bulk viscosity.
Eddy viscosity
In the study of turbulence in fluids, a common practical strategy for calculation is to ignore the small-scale vortices (or eddies) in the motion and to calculate a large-scale motion with an eddy viscosity that characterizes the transport and dissipation of energy in the smaller-scale flow (see large eddy simulation). Values of eddy viscosity used in modeling ocean circulation may be from 5x104 to 106 Pa·s depending upon the resolution of the numerical grid.
Fluidity
The reciprocal of viscosity is fluidity, usually symbolized by φ = 1 / η or F = 1 / η, depending on the convention used, measured in reciprocal poise (cm·s·g-1), sometimes called the rhe. Fluidity is seldom used in engineering practice.
The concept of fluidity can be used to determine the viscosity of an ideal solution. For two components a and b, the fluidity when a and b are mixed is

which is only slightly simpler than the equivalent equation in terms of viscosity:

where χa and χb is the mole fraction of component a and b respectively, and ηa and ηb are the components pure viscosities.
The linear viscous stress tensor
(See Hooke's law and strain tensor for an analogous development for linearly elastic materials.)
Viscous forces in a fluid are a function of the rate at which the fluid velocity is changing over distance. The velocity at any point  is specified by the velocity field
is specified by the velocity field  . The velocity at a small distance
. The velocity at a small distance  from point
from point  may be written as a Taylor series:
may be written as a Taylor series:

where 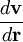 is shorthand for the dyadic product of the del operator and the velocity:
is shorthand for the dyadic product of the del operator and the velocity:

This is just the Jacobian of the velocity field. Viscous forces are the result of relative motion between elements of the fluid, and so are expressible as a function of the velocity field. In other words, the forces at 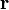 are a function of
are a function of  and all derivatives of
and all derivatives of  at that point. In the case of linear viscosity, the viscous force will be a function of the Jacobian tensor alone. For almost all practical situations, the linear approximation is sufficient.
at that point. In the case of linear viscosity, the viscous force will be a function of the Jacobian tensor alone. For almost all practical situations, the linear approximation is sufficient.
If we represent x, y, and z by indices 1, 2, and 3 respectively, the i,j component of the Jacobian may be written as  where
where  is shorthand for
is shorthand for  . Note that when the first and higher derivative terms are zero, the velocity of all fluid elements is parallel, and there are no viscous forces.
. Note that when the first and higher derivative terms are zero, the velocity of all fluid elements is parallel, and there are no viscous forces.
Any matrix may be written as the sum of an antisymmetric matrix and a symmetric matrix, and this decomposition is independent of coordinate system, and so has physical significance. The velocity field may be approximated as:

where Einstein notation is now being used in which repeated indices in a product are implicitly summed. The second term on the left is the asymmetric part of the first derivative term, and it represents a rigid rotation of the fluid about 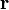 with angular velocity ω where:
with angular velocity ω where:

For such a rigid rotation, there is no change in the relative positions of the fluid elements, and so there is no viscous force associated with this term. The remaining symmetric term is responsible for the viscous forces in the fluid. Assuming the fluid is isotropic (i.e. its properties are the same in all directions), then the most general way that the symmetric term (the rate-of-strain tensor) can be broken down in a coordinate-independent (and therefore physically real) way is as the sum of a constant tensor (the rate-of-expansion tensor) and a traceless symmetric tensor (the rate-of-shear tensor):

where δij is the unit tensor. The most general linear relationship between the stress tensor 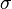 and the rate-of-strain tensor is then a linear combination of these two tensors (Landau & Lifshitz 1997):
and the rate-of-strain tensor is then a linear combination of these two tensors (Landau & Lifshitz 1997):

where ζ is the coefficient of bulk viscosity (or "second viscosity") and η is the coefficient of (shear) viscosity.
The forces in the fluid are due to the velocities of the individual molecules. The velocity of a molecule may be thought of as the sum of the fluid velocity and the thermal velocity. The viscous stress tensor described above gives the force due to the fluid velocity only. The force on an area element in the fluid due to the thermal velocities of the molecules is just the hydrostatic pressure. This pressure term (pδij) must be added to the viscous stress tensor to obtain the total stress tensor for the fluid.
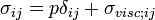
The infinitesimal force dFi on an infinitesimal area dAi is then given by the usual relationship:







![= I_0 {\left[ \operatorname{sinc} \left( \frac{\pi a}{\lambda} \sin \theta \right) \right] }^2](http://upload.wikimedia.org/math/8/7/9/879714a5b341089490d60a308e259848.png)
![I\left(\theta\right) = I_0 \left[ \operatorname{sinc} \left( \frac{\pi a}{\lambda} \sin \theta \right) \right]^2 \cdot \left[\frac{\sin\left(\frac{N\pi d}{\lambda}\sin\theta\right)}{\sin\left(\frac{\pi d}{\lambda}\sin\theta\right)}\right]^2](http://upload.wikimedia.org/math/4/8/e/48e0da4b6dab4360ab7699312bd07674.png)




 .
.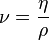 .
.




 ,
,

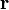 is specified by the velocity field
is specified by the velocity field  . The velocity at a small distance
. The velocity at a small distance  from point
from point 
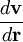 is shorthand for the dyadic product of the del operator and the velocity:
is shorthand for the dyadic product of the del operator and the velocity:
 where
where  is shorthand for
is shorthand for  . Note that when the first and higher derivative terms are zero, the velocity of all fluid elements is parallel, and there are no viscous forces.
. Note that when the first and higher derivative terms are zero, the velocity of all fluid elements is parallel, and there are no viscous forces.


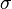 and the rate-of-strain tensor is then a linear combination of these two tensors
and the rate-of-strain tensor is then a linear combination of these two tensors